概述
本文主要介绍在以太坊中的签名问题,主要涵盖以下内容:
- ECDSA公钥密码学的数学原理与代码实现解析
- 以太坊客户端对交易信息签名的基本流程与源代码分析
- 智能合约内签名的验证
ECDSA公钥密码学
为了方便读者理解和实战本文中的内容,本文将结合一个可以使用Typescript编写用于生产环境的noble-secp256k1库作为实战案例解析。你可以在这里找到源代码。当然,为了节省篇幅,本文不会对此库中的所有代码进行解析。
公钥生成
以下内容部分参考了比特币 P2TR 交易详解。
在椭圆密码学中,许多不同种类的曲线都可以用于生成公钥。以太坊选择了与比特币相同的曲线类型,形式为y² = x³ + 7,被称为secp256k1。具体的图像如下图:
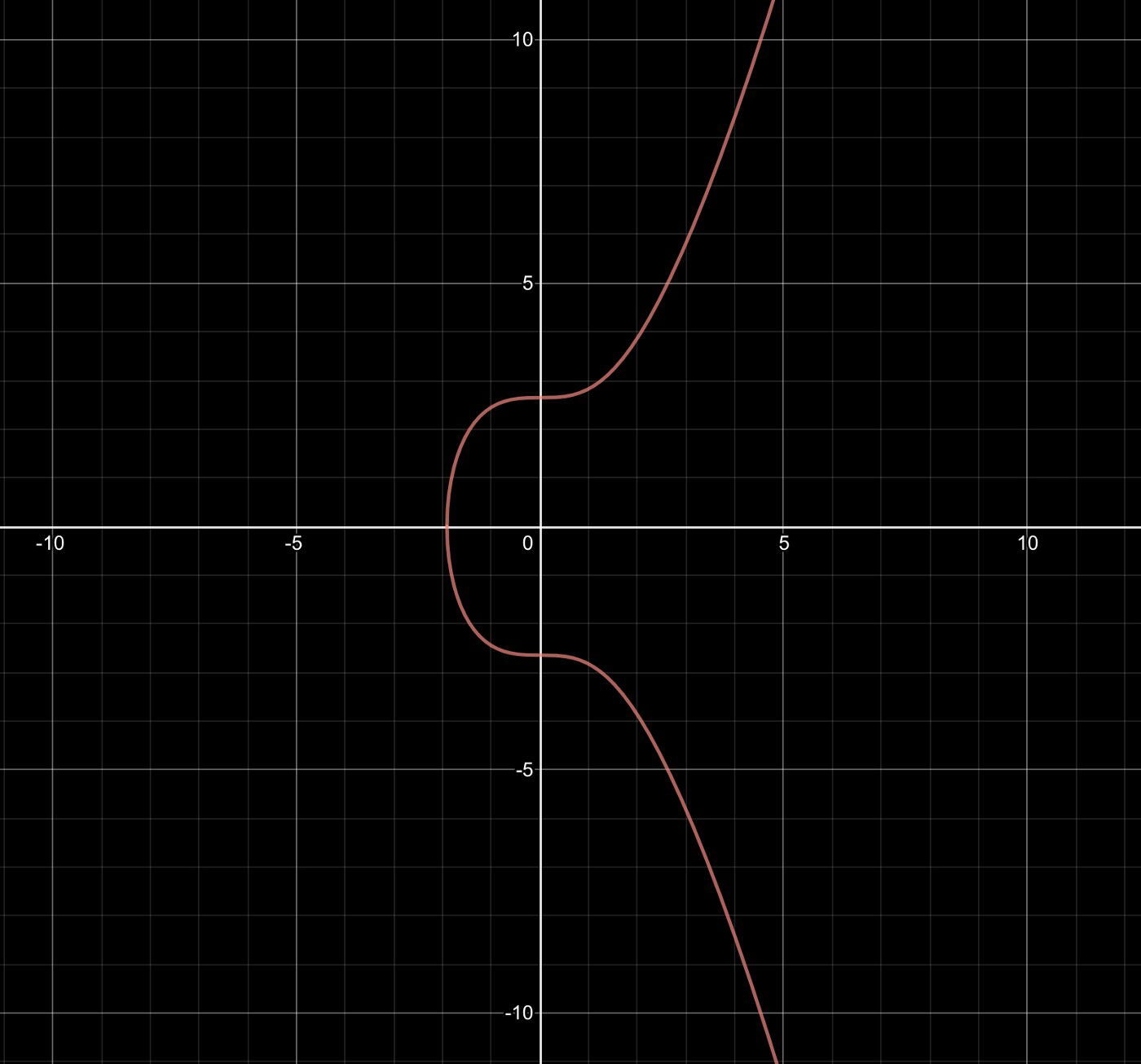
在此图像上,我们可以选择一个点作为生成点G,使用陷门函数计算获得公钥。陷门函数特点是正向计算简单,我们可以快速从私钥求出公钥,而逆向计算难度巨大。
比特币与以太坊均选择了一种被称为点倍增的陷门函数。如下图为我们选择的生成点G:
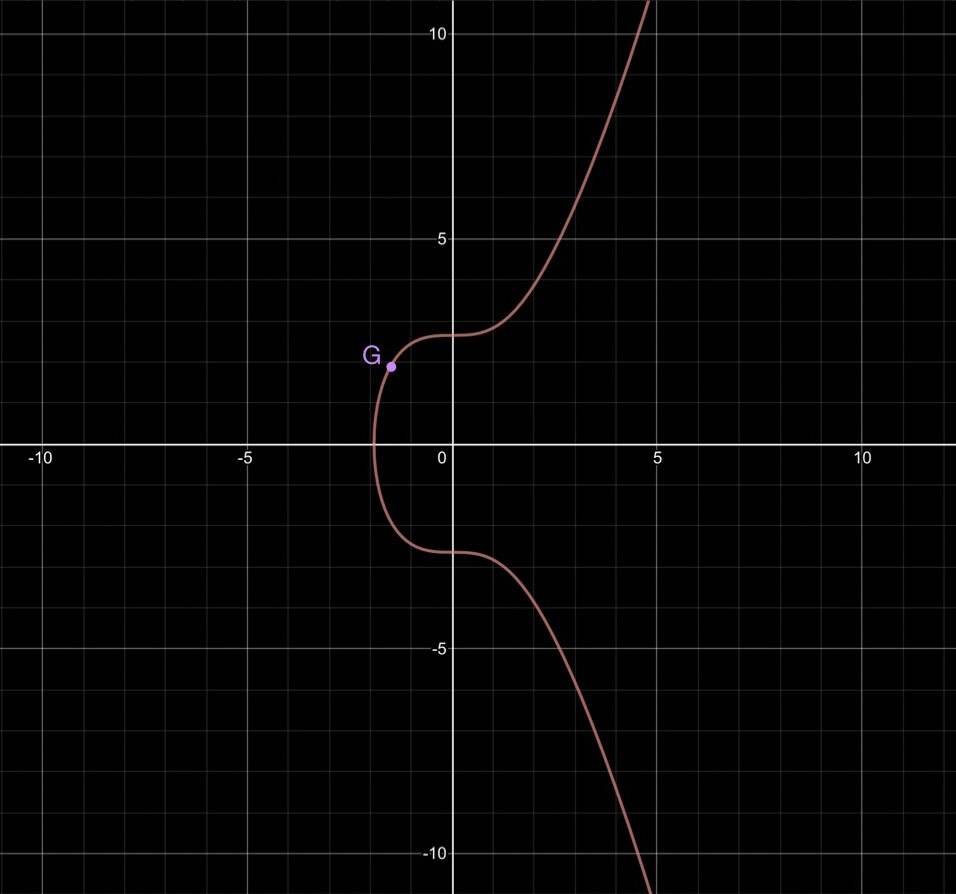
我们画出过点G的切线与曲线交与一点,我们选择此点关于x轴的对称点作为2G点。下图展示了进行第一次点倍增后的结果2G:
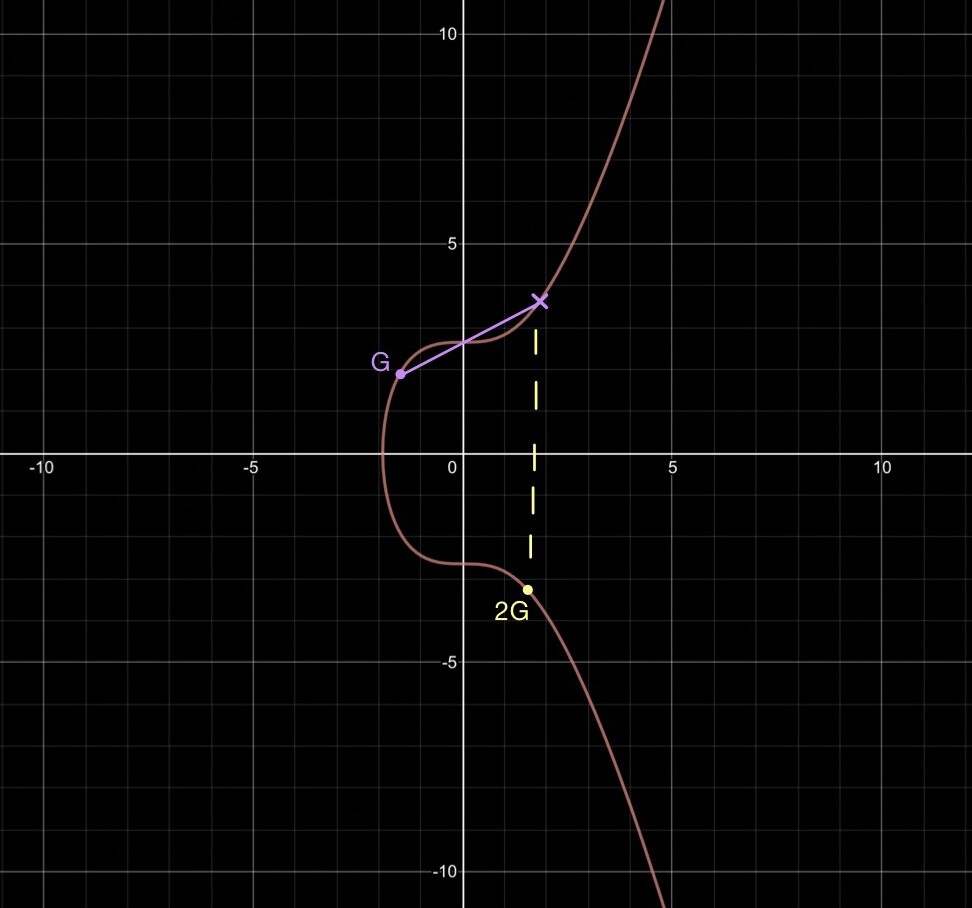
连结G与2G与曲线交与一点,我们选择与此点关于x轴对称的点作为3G。如下图:
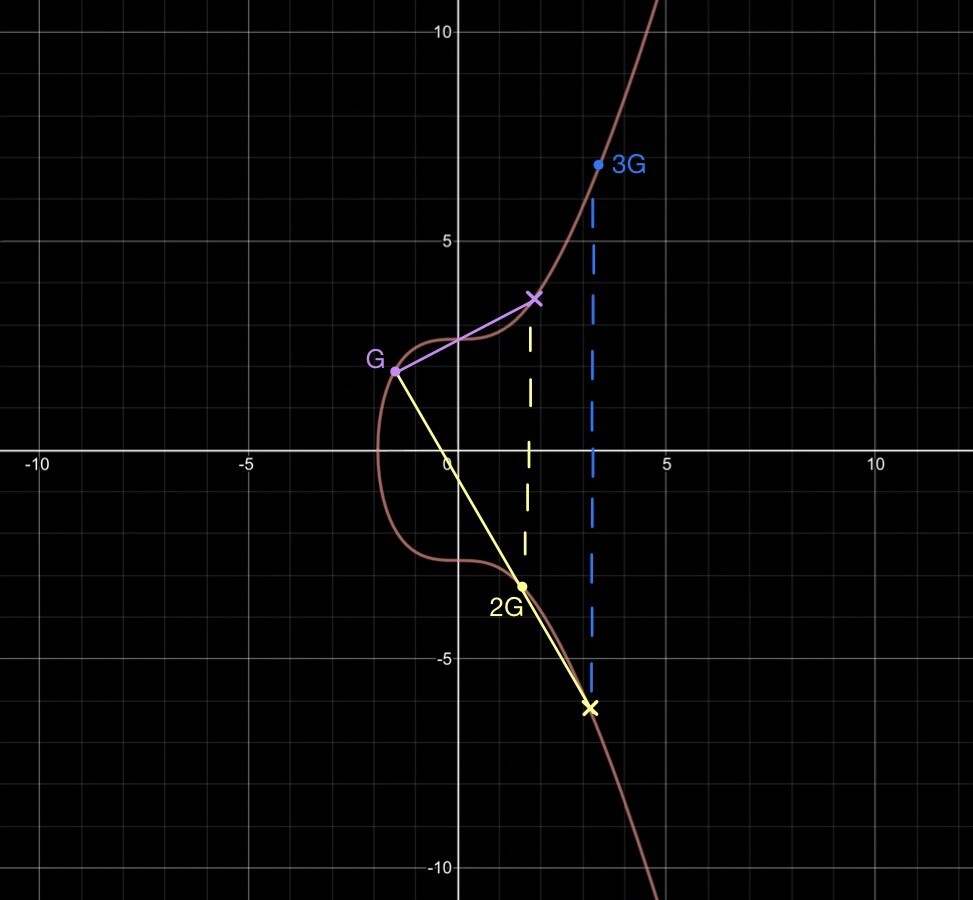
依次类推,我们可以得到4G的图像如下:
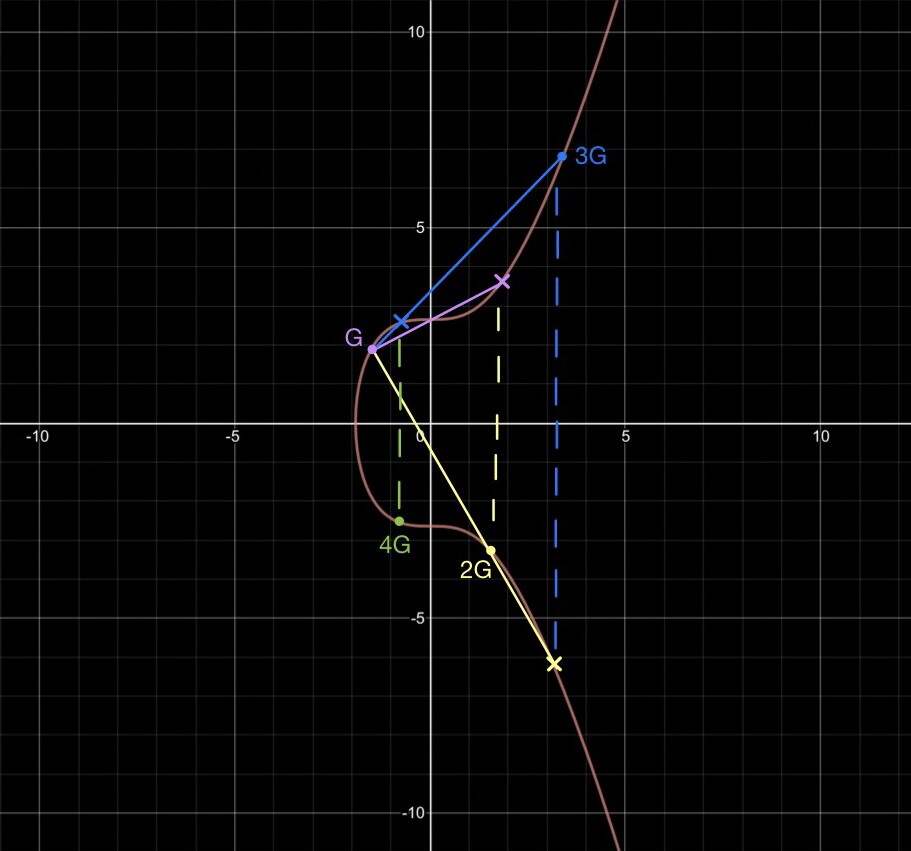
显然上述操作是直觉上是无法逆向的,关于严格的数学证明,读者可以自行查阅相关论文。以上过程可以进行算法上的优化,读者可以自行阅读noble-secp256k1的开发者的写的关于加速secp256k1计算的博客。
在此给出比特币规定的secp256k1的G的数值:
G.x = 0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
G.y = 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8
综上所述,当我们生成一个私钥d后,我可以通过计算P=dG获得公钥P,而以太坊账户就是选择公钥最后20 Bytes进行keccak-256计算得到的。
在noble-secp256k1实现如下:
static fromPrivateKey(privateKey: PrivKey) {
return Point.BASE.multiply(normalizePrivateKey(privateKey));
}
当然,上述代码中的multiply是经过优化的。Point.BASE即上文给出的G点。在代码中使用了bigint表示,定义如下:
Gx: BigInt('55066263022277343669578718895168534326250603453777594175500187360389116729240')
Gy: BigInt('32670510020758816978083085130507043184471273380659243275938904335757337482424')
当然,secp256k1也存在定义域,其最大值被记为n,任何有效的点都应在n之内。具体定义如下:
n: BigInt('0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141')
我们也可以在go-ethereum找到以下定义:
var (
secp256k1N, _ = new(big.Int).SetString("fffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141", 16)
secp256k1halfN = new(big.Int).Div(secp256k1N, big.NewInt(2))
)
签名
为了方便读者阅读,给出变量说明:
| 变量缩写 | 含义 |
|---|---|
| d | 私钥 |
| G | 生成点 |
| n | 曲线最大值 |
标准的ECDSA签名由两个整数r和s构成,签名流程如下:
- 对待签数据进行哈希计算获得哈希值
m - 生产随机数
k,并使用k与G相乘获得点R - 计算
r = R.x mod n。如果r = 0则需要重新生产随机数k - 计算
s = (1/k * (m + dr) mod n。如果s = 0则需要重新生产随机数k
上述过程中进行mod n是为了确保计算出的数值在我们所规定的定义域内。
在以太坊中,为了避免签名字段被其他应用使用,对哈希值m计算进行特别规定,即使用Keccak256("\x19Ethereum Signed Message:\n32" + Keccak256(message))进行哈希计算,使用go实现如下:
func signHash(data []byte) []byte {
msg := fmt.Sprintf("\x19Ethereum Signed Message:\n%d%s", len(data), data)
return crypto.Keccak256([]byte(msg))
}
对其签名的具体的代码实现方式如下:
function kmdToSig(kBytes: Uint8Array, m: bigint, d: bigint): RecoveredSig | undefined {
const k = bytesToNumber(kBytes);
if (!isWithinCurveOrder(k)) return;
// Important: all mod() calls in the function must be done over `n`
const { n } = CURVE;
const q = Point.BASE.multiply(k);
// r = x mod n
const r = mod(q.x, n);
if (r === _0n) return;
// s = (1/k * (m + dr) mod n
const s = mod(invert(k, n) * mod(m + d * r, n), n);
if (s === _0n) return;
const sig = new Signature(r, s);
const recovery = (q.x === sig.r ? 0 : 2) | Number(q.y & _1n);
return { sig, recovery };
}
上述代码给出了签名必要的两个元素r和s,通过这两个元素我们就可以得到一个完整的比特币签名。根据BIP66规定,比特币的签名组成如下:
0x30 [total-length] 0x02 [R-length] [R] 0x02 [S-length] [S]
我们可以通过上述代码给出的sig变量中的信息填充上述签名。
但在以太坊中,以太坊要求的签名格式如下:
[R][S][V]
其中增加了变量v,此值已在上文的代码中给出,为recovery值。但与尚未给出的通用recover不同,以太坊交易签名中的v为CHAIN_ID * 2 + 35或CHAIN_ID * 2 + 36,分别对应v=0和v=1。此过程由EIP155规定,目的是为了防止签名层面的重放攻击。
CHAIN_ID即每一条区块链的专属ID,具体可参考ChianList
验证签名
验证签名需要对签名者的公钥进行恢复,具体的流程如下:
- 计算签名信息的哈希值
m - 计算点
R = (x, y)。其中,当v=0时,x=r; 当v=1时,x=r+n - 计算
u1 = hs^-1 mod n,其中h为经过调整的哈希值,调整算法参考truncateHash - 计算
u2 = sr^-1 mod n - 计算
Q = u1 * G + u2 * R,Q即签名者的公钥。
我们在此给出对应的实现代码:
static fromSignature(msgHash: Hex, signature: Sig, recovery: number): Point {
msgHash = ensureBytes(msgHash);
const h = truncateHash(msgHash);
const { r, s } = normalizeSignature(signature);
if (recovery !== 0 && recovery !== 1) {
throw new Error('Cannot recover signature: invalid recovery bit');
}
if (h === _0n) throw new Error('Cannot recover signature: msgHash cannot be 0');
const prefix = recovery & 1 ? '03' : '02';
const R = Point.fromHex(prefix + numTo32bStr(r));
const { n } = CURVE;
const rinv = invert(r, n);
// Q = u1⋅G + u2⋅R
const u1 = mod(-h * rinv, n);
const u2 = mod(s * rinv, n);
const Q = Point.BASE.multiplyAndAddUnsafe(R, u1, u2);
if (!Q) throw new Error('Cannot recover signature: point at infinify');
Q.assertValidity();
return Q;
}
对于上述代码,基本逻辑与我们介绍的流程是相同的。但开发者为了优化代码使用了许多函数,这些函数大多包含位移、算法优化和增强安全性的内容,我们不在此深入研究。开发者将所有的代码都放在了index.ts中,读者可以仅下载index.ts,然后自行使用vscode阅读代码,请善用函数定义跳转功能F12。
通过上述流程,我们可以获得信息签名者的公钥,进一步可以获得签名者的以太坊地址。
以太坊交易签名
在go-ethereum中,我们可以查到以下关于交易签名的源代码:
// SignTx signs the transaction using the given signer and private key.
func SignTx(tx *Transaction, s Signer, prv *ecdsa.PrivateKey) (*Transaction, error) {
h := s.Hash(tx)
sig, err := crypto.Sign(h[:], prv)
if err != nil {
return nil, err
}
return tx.WithSignature(s, sig)
}
代码中最为关键的部分是s.Hash(tx)。从函数的参数中,我们可以得到s为Signer类型。跳转定义,我们发现Signer为接口类型,具体代码如下:
type Signer interface {
// Sender returns the sender address of the transaction.
Sender(tx *Transaction) (common.Address, error)
// SignatureValues returns the raw R, S, V values corresponding to the
// given signature.
SignatureValues(tx *Transaction, sig []byte) (r, s, v *big.Int, err error)
ChainID() *big.Int
// Hash returns 'signature hash', i.e. the transaction hash that is signed by the
// private key. This hash does not uniquely identify the transaction.
Hash(tx *Transaction) common.Hash
// Equal returns true if the given signer is the same as the receiver.
Equal(Signer) bool
}
出现Signer接口的原因是为了适配以太坊的升级,在以太坊升级过程中,开发者升级过多次签名流程中的tx交易数据结构。为了保证代码的简洁性,引入了接口类型。在代码中,对此接口的实现是根据区块高度决定的:
// MakeSigner returns a Signer based on the given chain config and block number.
func MakeSigner(config *params.ChainConfig, blockNumber *big.Int) Signer {
var signer Signer
switch {
case config.IsLondon(blockNumber):
signer = NewLondonSigner(config.ChainID)
case config.IsBerlin(blockNumber):
signer = NewEIP2930Signer(config.ChainID)
case config.IsEIP155(blockNumber):
signer = NewEIP155Signer(config.ChainID)
case config.IsHomestead(blockNumber):
signer = HomesteadSigner{}
default:
signer = FrontierSigner{}
}
return signer
}
London、BerLin都是以太坊的阶段代号,具体可以参考The history of Ethereum
由于我们没有必要使用以前Signer,在此处我们仅介绍最新的实现londonSigner。此签名器满足以下标准:
- EIP-1599,详情参看以太坊机制详解:Gas Price计算
- EIP-2930,增加了
accessList参数,预支付存储费用 - EIP-155,增加
CHAIN_ID参数,防止重放攻击
我们所需要研究的函数如下:
func (s londonSigner) Hash(tx *Transaction) common.Hash {
if tx.Type() != DynamicFeeTxType {
return s.eip2930Signer.Hash(tx)
}
return prefixedRlpHash(
tx.Type(),
[]interface{}{
s.chainId,
tx.Nonce(),
tx.GasTipCap(),
tx.GasFeeCap(),
tx.Gas(),
tx.To(),
tx.Value(),
tx.Data(),
tx.AccessList(),
})
}
其中,tx.Type()有以下几种情况:
const (
LegacyTxType = iota
AccessListTxType
DynamicFeeTxType
)
为了降低复杂度,我们自此不再讨论tx.Type() != DynamicFeeTxType的情况,这种情况并不符合EIP-1599。从代码中可以看出核心函数为prefixedRlpHash,其定义如下:
func prefixedRlpHash(prefix byte, x interface{}) (h common.Hash) {
sha := hasherPool.Get().(crypto.KeccakState)
defer hasherPool.Put(sha)
sha.Reset()
sha.Write([]byte{prefix})
rlp.Encode(sha, x)
sha.Read(h[:])
return h
}
简化来说,此代码首先完成了在sha变量内写入0x02标识符,此标识符表示该交易符合EIP1599。
然后,继续在sha变量内写入交易数据的rlp编码,如下:
rlp([chain_id, nonce, max_priority_fee_per_gas, max_fee_per_gas, gas_limit, destination, amount, data, access_list])
最后进行哈希计算。
获得符合要求的哈希值后,我们只需要对此哈希值按照上述方法进行签名即可,注意我们需要V、R、S依次进行编码加入交易数据即可。其中, V和R长度为32 bytes, S长度为1 bytes.
所有流程可以用下图表示:
验证签名只需要将上述过程反过来进行,较为简单,此处不再赘述。
链上签名验证
基本代码
请读者阅读以下代码:
function recoverSignerFromSignature(uint8 v, bytes32 r, bytes32 s, bytes32 hash) external {
address signer = ecrecover(hash, v, r, s);
require(signer != address(0), "ECDSA: invalid signature");
}
这是使用ecrecover的一个代码示例,基本展示了我们使用ecrecover的基本方法,但在实际中,我们需要更多的代码确保安全。不要将此代码用于生产环境。我们会在本文的最后给出生产环境中应使用的代码。
通过上文学习,相信读者很快就能判断出ecrecover的作用,该指令接受hash、v、r和s用于恢复签名者公钥。
特殊的一点是ecrecover是一个预编译的EVM指令。预编译意味着智能合约的通用功能已被EVM底层实现,运行EVM的节点可以更加有效地运行含有此类代码的智能合约,而且与自己实现的代码相比,性能更高且消耗的gas费更少。
你可以在EVM Codes查询到此指令。
适用范围
ecrecover适合所用使用标准secp256k1曲线签名的数据,但我们建议使用以太坊目前最常用的签名API进行签名:
- eth_sign
- personal_sign
- EIP-712
以上API均在metamask中进行了实现,具体使用方法可以参考文档。
其中EIP712属于一种较新的签名标准,在metamask中的实现为signTypedData_v4。我们会在后文详细讨论此标准及其应用。
eth_sign用于对任何数据进行签名,但不建议开发者使用它完成非交易数据签名。这会导致严重的安全问题。
personal_sign也可以对任一数据进行签名,但使用此API会自动在代签数据前加入前缀\x19Ethereum Signed Message:\n,以防止此签名被用于交易。目前常用于网站的登录。
目前,metamask推荐开发者使用EIP712进行数据签名,而且metamask还对这种方法进行特殊支持,如UI显示等。另一方面,EIP712在复杂数据交互方面具有先天优势,索引开发者应尽可能使用EIP712。
EIP712
对于DApp签名相关问题,以太坊标准已经有EIP712进行了相关规范。我们之前在MetaMask一键登录设计已经讨论过链下EIP712。但其实EIP712主要解决了链上智能合约签名与验证的相关问题。
签名
EIP712的核心内容是结构化数据的哈希计算,与一般的交易数据不同,EIP712主要面向DApp等相关产品,如果采用与交易数据相同的签名模式,可能导致在不同DApp之间签名被盗用。比如A产品使用一组数据进行哈希签名,而B产品也选择了与A产品相同的数据结构,这意味着你在A产品内进行的非交易签名可以在B产品内使用。这极有可能造成严重的财产问题。
为了解决此问题,EIP712对结构化数据的哈希使用了以下公式:
hashStruct(s : 𝕊) = keccak256(typeHash ‖ encodeData(s))
typeHash = keccak256(encodeType(typeOf(s)))
上述公式中𝕊代表结构化类型数据集中的所有实例
为了方便读者理解EIP712进行结构化数据的流程,我们在此给出一个结构化数据:
struct Mail {
address from;
address to;
string contents;
}
下述给出的‖代表字节拼接。
encodeType要求数据被编码为type ‖ " " ‖ name。上述示例应被编码为Mail(address from,address to,string contents),与我们在使用多种方式编写可升级的智能合约(下)中讨论的函数选择器字符串编码的规则类似。此处应该注意type必须是solidity规定的数据类型。
上述对
type的描述较为简陋,但一般情况下可以理解为就是solidity中的数据类型,实际上,不是所有的数据类型都可以编码在EIP712中,具体情况可以参考标准定义
encodeData定义为enc(value₁) ‖ enc(value₂) ‖ … ‖ enc(valueₙ)。enc代表编码函数,要求数据编码成32 bytes,编码要求大致如下:
- 布尔值使用
uint256表示,0代表false,1代表true address编码为uint160uint统一编码为uint256,并使用大端顺序排序bytes1到bytes32数据类型使用0填充为bytes32bytes和string均进行keccak256后编码array类型数据进行keccak256后编码struct类型数据递归调用hashStruct函数
上述规则与abi编码规则是基本一致的,但在string等类型上存在区别,请注意对比。
注意
bytes1,bytes2,…,bytes32等数据类型属于不可变的长度固定静态类型,而bytes则属于长度可变的动态类型,注意区分。
经过上述步骤我们其实仍没有解决签名盗用问题,为了解决这一问题,EIP712要求最终的需要待签数据应该为以下形式:
encode(domainSeparator : 𝔹²⁵⁶, message : 𝕊) = "\x19\x01" ‖ domainSeparator ‖ hashStruct(message)
在此处,EIP712引入了一个重要的待签字段domainSeparator,它的定义如下:
domainSeparator = hashStruct(eip712Domain)
eip712Domain规定由以下字段构成:
string name,具有可读性的合约名称等string version,当前交互的dapp或合约的版本,不同版本之间的签名不能混用uint256 chainId,区块链链ID,参考此网站address verifyingContract,验证签名的合约,可以保证签名仅被单一合约使用,选填bytes32 salt,加盐,可选填
注意不应更改或删除上述字段,如果你有新的建议,请提出
EIP请求。
我们在此处列出一个简单的流程图解释上述过程:
在上图中,我们省略了encodeData的详细情况。
标准中也给出了与对应接口eth_signTypedData交互时应使用的json-schema:
{
type: 'object',
properties: {
types: {
type: 'object',
properties: {
EIP712Domain: {type: 'array'},
},
additionalProperties: {
type: 'array',
items: {
type: 'object',
properties: {
name: {type: 'string'},
type: {type: 'string'}
},
required: ['name', 'type']
}
},
required: ['EIP712Domain']
},
primaryType: {type: 'string'},
domain: {type: 'object'},
message: {type: 'object'}
},
required: ['types', 'primaryType', 'domain', 'message']
}
我们在此给出一个完整的示例:
{
domain: {
// Defining the chain aka Rinkeby testnet or Ethereum Main Net
chainId: 1,
// Give a user friendly name to the specific contract you are signing for.
name: 'Ether Mail',
// If name isn't enough add verifying contract to make sure you are establishing contracts with the proper entity
verifyingContract: '0xCcCCccccCCCCcCCCCCCcCcCccCcCCCcCcccccccC',
// Just let's you know the latest version. Definitely make sure the field name is correct.
version: '1',
},
// Defining the message signing data content.
message: {
/*
- Anything you want. Just a JSON Blob that encodes the data you want to send
- No required fields
- This is DApp Specific
- Be as explicit as possible when building out the message schema.
*/
contents: 'Hello, Bob!',
attachedMoneyInEth: 4.2,
from: {
name: 'Cow',
wallets: [
'0xCD2a3d9F938E13CD947Ec05AbC7FE734Df8DD826',
'0xDeaDbeefdEAdbeefdEadbEEFdeadbeEFdEaDbeeF',
],
},
to: [
{
name: 'Bob',
wallets: [
'0xbBbBBBBbbBBBbbbBbbBbbbbBBbBbbbbBbBbbBBbB',
'0xB0BdaBea57B0BDABeA57b0bdABEA57b0BDabEa57',
'0xB0B0b0b0b0b0B000000000000000000000000000',
],
},
],
},
// Refers to the keys of the *types* object below.
primaryType: 'Mail',
types: {
// TODO: Clarify if EIP712Domain refers to the domain the contract is hosted on
EIP712Domain: [
{ name: 'name', type: 'string' },
{ name: 'version', type: 'string' },
{ name: 'chainId', type: 'uint256' },
{ name: 'verifyingContract', type: 'address' },
],
// Not an EIP712Domain definition
Group: [
{ name: 'name', type: 'string' },
{ name: 'members', type: 'Person[]' },
],
// Refer to PrimaryType
Mail: [
{ name: 'from', type: 'Person' },
{ name: 'to', type: 'Person[]' },
{ name: 'contents', type: 'string' },
],
// Not an EIP712Domain definition
Person: [
{ name: 'name', type: 'string' },
{ name: 'wallets', type: 'address[]' },
],
},
}
另一个示例可以参考我之前的博客MetaMask一键登录设计。此博客使用了EIP712开发了一个链下登陆系统。
对于EIP712标准,大多数钱包都进行了实现,此处我们主要介绍MetaMask钱包。该钱包提供了signTypedData_v4方法以支持EIP712,读者可自行阅读(文档)[https://docs.metamask.io/guide/signing-data.html#sign-typed-data-v4]
验证
通过上文,我们得到了EIP712签名的基本形式:
"\x19\x01" ‖ domainSeparator ‖ hashStruct(message)
一般情况下,智能合约接收到的并不是完整的签名而是签名后的v, r, s数据和发送的结构体。故而我们需要先进行签名重建,一个简单的例子如下,你可以在这里找到完整代码:
function verify(Mail mail, uint8 v, bytes32 r, bytes32 s) internal view returns (bool) {
// Note: we need to use `encodePacked` here instead of `encode`.
bytes32 digest = keccak256(abi.encodePacked(
"\x19\x01",
DOMAIN_SEPARATOR,
hash(mail)
));
return ecrecover(digest, v, r, s) == mail.from.wallet;
}
用户将Mail结构体和v, r, s数据发送给智能合约,智能合约使用以上数据调用verify进行验证。在验证时,首先进行签名重建,在检验签名者是否为mail的发送者。
关于hash函数读者可自行查阅源代码,注意此文中给出的hash函数均符合以下公式:
hashStruct(s : 𝕊) = keccak256(typeHash ‖ encodeData(s))
typeHash = keccak256(encodeType(typeOf(s)))
在此举出一个例子:
struct Person {
string name;
address wallet;
}
bytes32 constant PERSON_TYPEHASH = keccak256(
"Person(string name,address wallet)"
);
function hash(Person memory person) internal pure returns (bytes32) {
return keccak256(abi.encode(
PERSON_TYPEHASH,
keccak256(bytes(person.name)),
person.wallet
));
}
在进行hash时,首先使用PERSON_TYPEHASH完成typeHash定义。然后再结构化各个数据。比如对string类型的person.name进行keccak转换。 读者可能发现似乎没有对person.wallet进行转换,这是因为abi.encode会自动进行此类转换。
默认的
abi.encode会对string计算utf-8编码,而EIP712规定为计算keccak,所以此处需要手动转换。判断是否需要手动转换的方法就是对比abi的encode规则与EIP712的规定是否一致。前者请查阅Formal Specification of the Encoding,后者请查阅Definition of encodeData
上述代码使用了abi.encode方法,该方法会自动转换所有变量使其符合编码规则并进行拼接操作。但是,根据以下公式:
encode(domainSeparator : 𝔹²⁵⁶, message : 𝕊) = "\x19\x01" ‖ domainSeparator ‖ hashStruct(message)
最终的代签数据中包含\x19\x01数据,如果使用abi.encode进行拼接,那么\x19\x01会被转换为bytes32形式,进而导致生成的哈希值错误。为了避免这一问题,我们使用了abi.encodePacked方法。此方法不会对string进行标准abi编码,而仅仅将其转换为utf-8。使用此函数可以保证最终生成的哈希值正确的。
如果你仍无法理解上述内容,请参考Solidity Tutorial: all about ABI
有读者可能疑惑为什么不直接发送完整的签名,因为智能合约往往需要
一个例子
我们在上述流程中,我们已经完成了一个简单的项目。但我们会在此节使用openzeppelin简化这一流程并提高安全性。
本项目的所有代码均放在Github仓库中找到。
我们此处仍使用此数据作为待签数据:
{
contents: 'Hello, Bob!',
from: {
name: 'Cow',
wallet: '0xCD2a3d9F938E13CD947Ec05AbC7FE734Df8DD826',
},
to: {
name: 'Bob',
wallet: '0xbBbBBBBbbBBBbbbBbbBbbbbBBbBbbbbBbBbbBBbB',
}
}
合约编写
首先编写接口IProduct.sol。首先考虑数据结构,我们可以把from和to中的结构化数据抽离为Person结构体,把整体数据抽象为Mail结构体。然后,我们需要设计函数接口,在此处我们仅需要verify函数对外暴露,此函数仅需要Mail和signature参数。
具体代码如下:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.13;
interface IProduct {
struct Person {
string name;
address wallet;
}
struct Mail {
Person from;
Person to;
string contents;
}
function verify(Mail memory mail, bytes memory signature) external;
}
我们需要对此接口进行实现。首先完成合约的初始化,具体代码如下:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.13;
import "openzeppelin-contracts/contracts/utils/cryptography/draft-EIP712.sol";
import "openzeppelin-contracts/contracts/utils/cryptography/ECDSA.sol";
import "./IProduct.sol";
contract ProductEIP712 is EIP712, IProduct {
constructor(string memory _name, string memory _version)
EIP712(_name, _version)
{}
}
上述代码主要实现了EIP712Domain的初始化。值得注意的是,openzeppelin提供的EIP712Domain仅提供以下属性:
bytes32 typeHash = keccak256(
"EIP712Domain(string name,string version,uint256 chainId,address verifyingContract)"
);
在EIP712合约中,最关键的函数为:
function _hashTypedDataV4(bytes32 structHash) internal view virtual returns (bytes32) {
return ECDSA.toTypedDataHash(_domainSeparatorV4(), structHash);
}
此函数的返回值正是完整的EIP712哈希值结果。
我们需要生成此函数所需要的全部参数,_domainSeparatorV4()函数是库提供的,定义如下:
function _domainSeparatorV4() internal view returns (bytes32) {
if (address(this) == _CACHED_THIS && block.chainid == _CACHED_CHAIN_ID) {
return _CACHED_DOMAIN_SEPARATOR;
} else {
return _buildDomainSeparator(_TYPE_HASH, _HASHED_NAME, _HASHED_VERSION);
}
}
对此函数,我们不需要提供额外参数。
对于structHash参数,我们则需要自己进行计算。
读者可能疑惑为什么智能合约中的函数和
MetaMask的函数带有V4后缀,这是因为EIP712在形成标准期间进行过多次变化,V4是其最后标准。你可以查阅此注释了解更多。如果没有特殊情况,建议使用V4标准。
综上所述,我们需要定义一个符合EIP712规定的hashStruct函数。参考上文给出的计算方法,由于递归属性,我们需要首先定义Person的hashStruct,然后定义Mail的hashStruct,代码如下:
bytes32 constant PERSON_TYPEHASH =
keccak256("Person(string name,address wallet)");
bytes32 constant MAIL_TYPEHASH =
keccak256(
"Mail(Person from,Person to,string contents)Person(string name,address wallet)"
);
function hash(Person memory person) internal pure returns (bytes32) {
return
keccak256(
abi.encode(
PERSON_TYPEHASH,
keccak256(bytes(person.name)),
person.wallet
)
);
}
function hash(Mail memory mail) public pure returns (bytes32) {
return
keccak256(
abi.encode(
MAIL_TYPEHASH,
hash(mail.from),
hash(mail.to),
keccak256(bytes(mail.contents))
)
);
}
上述代码符合以下公式:
hashStruct(s : 𝕊) = keccak256(typeHash ‖ encodeData(s))
typeHash = keccak256(encodeType(typeOf(s)))
有了上述参数,我们最终可以编写verify函数,具体定义如下:
function verify(Mail memory mail, bytes memory signature) public {
bytes32 digest = _hashTypedDataV4(hash(mail));
address signer = ECDSA.recover(digest, signature);
require(signer == msg.sender, "Not sender");
}
在此处,我们使用了安全性更高的ECDSA.recover函数。
编写测试
一种方案是由foundry官方文档提供的,读者可以自行参考文档。
另一种方案比较神奇,我们从浏览器端获得签名结果,然后前往测试合约中进行测试。
编写测试合约,在test/EIP712/product.t.sol中输入:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.13;
import "forge-std/Test.sol";
import "../../src/EIP-712/product.sol";
import "../../src/EIP-712/IProduct.sol";
contract ProductTest is Test {
ProductEIP712 private product;
function setUp() public {
product = new ProductEIP712("Ether Mail", "1");
}
function testArg() public {
vm.chainId(4);
console2.log(address(product));
}
}
上述合约主要为我们提供一些必要的参数,主要是verifyingContract参数。当然,在此处,我们使用vm.chainId(4);将链ID改为了4,即Rinkeby网络。
在终端内使用forge test -vvv,获得以下输出:

前往此网页,首先点击Connected链接钱包,然后点击ETH_ACCOUNTS查看地址是否正确。按下F12打开开发者工具,进入Console终端。
键入window.ethereum,返回值应不为空。
首先设置待签数据,输入下文代码:
const msgParams = JSON.stringify({
domain: {
name: 'Ether Mail',
chainId: 4,
version: '1',
verifyingContract: '0xce71065d4017f316ec606fe4422e11eb2c47c246',
},
message: {
contents: 'Hello, Bob!',
from: {
name: 'Cow',
wallet: '0xCD2a3d9F938E13CD947Ec05AbC7FE734Df8DD826',
},
to: {
name: 'Bob',
wallet:
'0xbBbBBBBbbBBBbbbBbbBbbbbBBbBbbbbBbBbbBBbB',
},
},
primaryType: 'Mail',
types: {
EIP712Domain: [
{ name: 'name', type: 'string' },
{ name: 'version', type: 'string' },
{ name: 'chainId', type: 'uint256' },
{ name: 'verifyingContract', type: 'address' },
],
Mail: [
{ name: 'from', type: 'Person' },
{ name: 'to', type: 'Person' },
{ name: 'contents', type: 'string' },
],
Person: [
{ name: 'name', type: 'string' },
{ name: 'wallet', type: 'address' },
],
},
});
其中,chainId请根据页面显示确定。verifyingContract地址根据上文终端输出决定。
使用下述命令进行签名:
const sign = await ethereum.request({
method: 'eth_signTypedData_v4',
params: ["0x11475691C2CAA465E19F99c445abB31A4a64955C", msgParams],
});
其中,params第一个参数应改为个人地址。
键入sign,输出结果如下:
0x70aa843f69e5d32252c65011b34831e79c9c64752134d9318cdefb7f8d7a04ac08a2193aedb8f329a8d80f5390c7f661fe447ccc9337ebed15b578c01d7dc71e1c
获得签名结果后,我们继续进行测试合约的编写,加入以下函数:
function testVerify() public {
vm.chainId(4);
vm.prank(0x11475691C2CAA465E19F99c445abB31A4a64955C);
bytes
memory Signature = hex"70aa843f69e5d32252c65011b34831e79c9c64752134d9318cdefb7f8d7a04ac08a2193aedb8f329a8d80f5390c7f661fe447ccc9337ebed15b578c01d7dc71e1c";
IProduct.Person memory PersonFrom = IProduct.Person({
name: "Cow",
wallet: address(0xCD2a3d9F938E13CD947Ec05AbC7FE734Df8DD826)
});
IProduct.Person memory PersonTo = IProduct.Person({
name: "Bob",
wallet: address(0xbBbBBBBbbBBBbbbBbbBbbbbBBbBbbbbBbBbbBBbB)
});
IProduct.Mail memory mail = IProduct.Mail({
contents: "Hello, Bob!",
from: PersonFrom,
to: PersonTo
});
product.verify(mail, Signature);
vm.stopPrank();
}
其中,vm.prank(address)用于切换地址。
最后,在终端内输入forge test,结果如下:

EIP-1271
我们在上文给出的签名方式都是由用户使用私钥进行签名的情况。在智能合约日益发展的今天,我们需要有一种方式实现合约签名。但众所周知,智能合约没有自己的私钥,我们只能通过一些特殊的方式实现类似签名的效果。这一方式已经被EIP1271进行了相关的规范化。当然,EIP1271仍依赖于用户私钥进行签名的步骤。
为了方便读者后文理解代码,我们在此处首先给出使用EIP1271的流程:
- 合约钱包拥有者使用自己的私钥进行签名;
- 向目标合约提交合约钱包拥有者的签名
- 目标合约使用此签名向合约钱包进行
isValidSignature方法。 - 合约钱包中的
isValidSignature方法会检查签名是否属于合约拥有者。如果属于,合约钱包返回0x1626ba7e,否则返回0xffffffff - 目标合约接受返回值,通过签名正误决定下一步操作
在上述过程中,谁可以使用私钥进行签名代表合约签名是可以通过合约编程修改确定的。上述流程的实质是合约将签名权委托授权给用户,由用户代表合约进行签名。
在此过程中,我们可以看到最重要的就是isValidSignature方法,其定义如下:
function isValidSignature(
bytes32 _hash,
bytes calldata _signature
) external override view returns (bytes4) {
// Validate signatures
if (recoverSigner(_hash, _signature) == owner) {
return 0x1626ba7e;
} else {
return 0xffffffff;
}
}
对于recoverSigner需要根据具体的签名类型由用户自行编写,较为简单的方法是使用ecrecover。
而在目标合约中,我们需要实现调用isValidSignature的函数如下:
function callERC1271isValidSignature(
address _addr,
bytes32 _hash,
bytes calldata _signature
) external view {
bytes4 result = IERC1271Wallet(_addr).isValidSignature(_hash, _signature);
require(result == 0x1626ba7e, "INVALID_SIGNATURE");
}
通过上述步骤,我们就可以实现对合约签名进行校验。一个具体的例子是GnosisSafe支持EIP1271标准的合约签名,具体代码可以参考这里。
总结
本文介绍了基本的EIP712的原理和相关链上和链下合约。我们会在未来编写一篇介绍了EIP712的进一步应用的文章。
拓展阅读
- 比特币 P2TR 交易详解,介绍了比特币使用的
ECDSA和schnorr多签名等内容 - A (Relatively Easy To Understand) Primer on Elliptic Curve Cryptography,由Cloudflare编写的博客,介绍了部分历史和椭圆函数密码学在网络安全中的应用
- 以太坊技术与实现 签名与校验,完整介绍了以太坊的签名和验证等相关问题,同时给出
go编写的以太坊底层代码 - 以太坊签名验签原理揭秘,此文较短但也基本全面介绍了以太坊内的签名和验证,可以作为上一篇文章的缩减版
- Elliptic Curve Digital Signature Algorithm,维基百科,给出了完整的数学证明

