概述
纯链上资产定价是一项相当有趣的工作,常见的方案都是基于函数报价。具体来说,包含以下三类:
- 各类用于代币互换的 AMM 曲线,以 Uniswap 推出的 x * y = k 最为著名
- 直接根据供应量等因子给出报价的 Bonding Curve 方案,近期的 FriendTech 和 pump.fun 都属于此类
- 基于拍卖的方案,链上拍卖方案往往使用荷兰式拍卖以提高效率,较少见到因英式拍卖,且由于技术问题,也较难见到基于密封报价的盲拍。较为著名的是 paradigm 推出的 GDA 和 VRGDA 方案,以及 UniswapX 内的荷兰式拍卖方案
上述不同的函数定价方案都存在一定的优点和缺陷,本文将首先介绍这些目前已经被广泛使用的链上资产定价方案,然后本文将介绍基于 ERC7527 及连续函数报价的新一代链上资产定价方案。
AMM 曲线
目前在纯链上定价方案中,被最广泛使用的和目前最具有共识的定价方案就是 AMM 定价。对于 AMM 定价而言,最为著名的方案就是 x * y = k 的定价曲线,该曲线由 Uniswap 首次引入。
该公式内的 $x$ 指 x 资产在池子内的余额,而 $y$ 代表 y 资产在池子内的余额,而 $k$ 是一个常量。其对应的 代码 如下:
uint balance0Adjusted = balance0.mul(1000).sub(amount0In.mul(3));
uint balance1Adjusted = balance1.mul(1000).sub(amount1In.mul(3));
require(balance0Adjusted.mul(balance1Adjusted) >= uint(_reserve0).mul(_reserve1).mul(1000**2), 'UniswapV2: K');
上述代码内存在四个变量,其含义如下:
balance0Adjusted用户向池子里发送 x 资产后,池子里的 x 资产的数量减去发送给池子的 x 资产的 0.3% 的手续费balance1Adjusted用户向池子里发送 y 资产后,池子里的 y 资产的数量减去发送给池子的 y 资产的 0.3% 的手续费_reserve0x 资产在池子内部的储备_reserve1y 资产在池子内部的储备
我们可以以一个实际的案例介绍上述代码的工作原理。假如池子内目前包含 20000DAI / 10 WETH 的储备,我们希望使用 1 WETH 兑换 1500 DAI,计算过程如下:
_reserve0 = 20000 DAI
_reserve1 = 10 WETH
k = 20000 * 10 = 200000
上述是在进行 1 WETH 兑换 1500 DAI 之前的资金储备,然后我们进行以下兑换:
balance0 = 20000 - 1500 = 18500
balance1 = 10 + 1 = 11
amount0In = 0
amount1In = 1
balance0Adjusted = 18500
balance1Adjusted = 11 - (1 * 0.003) = 10.997
newK = balance0Adjusted * balance1Adjusted = 203444.5
此时 newK 大于 k 的条件成立,所以兑换可以正常进行。当然很多用户可以感觉似乎没有接触过这种兑换方式,而是直接给定 1 WETH ,Uniswap 前端就会显示 1 WETH 可以兑换的最大 DAI 的数量,这是基于 newK = k 和池子内储备金的数量计算出来的,假如用户使用给定 x 单位资产兑换 y 单位的另一种资产,可以兑换的最大数量的具体公式推导如下:
$$
(x + dx)(y - dy) = xy \\
y - dy = \frac{xy}{(x + dx)} \\
dy = y - \frac{xy}{(x + dx)}
$$
此处的 $dx$ 即用户给出的资产数额,而 $dy$ 即用户付出 x 资产获得的 y 资产的数量,而 $x$ 和 $y$ 则为兑换时池子内部的储备。下图展示了一次基于 x * y = k 的代币交换的可视化展示:
对于 AMM 曲线方案而言,该方案最大的优点在于:
- 最为目前最为广泛使用的代币互换方案,AMM 曲线具有强共识
- 对于 ERC20 兑换,AMM 曲线方案是目前最优的解决方案
但是 AMM 曲线也有其重要缺陷,其中最大的一个缺陷在于流动性提供方。对于 AMM 曲线的流动性提供方(下文使用 LP 缩写) 而言,面临以下几个问题:
- 流动性提供方的来源。由于对于刚刚发行的代币而言,代币发行方必须为代币提供初始流动性以保证用户的兑换。对于后续流动性的来源是较难保证的,而且第三方的流动性提供方甚至代币发行方都有可能撤回 LP 使得 AMM 池内的流动性迅速丧失
- 流动性的管理。伴随着对 AMM 曲线的研究深入,发现了一系列可能导致 LP 损失的因素,比如大名鼎鼎的无常损失(Impermanent Loss)。这导致 LP 管理变成了一项复杂工作。
- MEV 的恶意攻击。在以太坊内,对 AMM 曲线的 MEV 是极其发达的,大部分 MEV 操作都会使得不同的参与方受损。比较恶意的对 AMM 曲线的 MEV 是三明治攻击,对于任何不设置滑点的交易,都会被三明治攻击,最终的结果是用户损失大量资产。
实际上,对于使用 AMM 曲线作为资产定价的最大问题仍是在于初始流动性的提供,对于早期项目方而言,发行资产一定需要大量的资产进行初始流动性提供,对于 Meme 币项目方而言,在非 FOMO 的时间节点很难有充足的流动性。
当然,AMM 曲线的另一个特性是只能对 ERC20 资产对进行定价,使用 AMM 曲线对 NFT 等资产进行定价则需要使用一些特殊方案,这些 AMM 曲线定价 NFT 的方案究其本质都是使用了 NFT 碎片化的思想,比如 ERC404 资产,我们很难真正的称这些由 AMM 曲线定价的 NFT 是一个真正的 NFT。
Bonding Curve
Bonding Curve 是一个在早期加密领域被广泛讨论的话题,其全程为 Token Bonding Curve,一般来说包含以下参数:
供应代币。Bonding Curve 资金池的底层资产。一般来说允许用户向资金池内使用供应代币购买发行代币;部分情况下,也可以反向操作,即向池子卖出发行代币换取供应代币。一般情况下,供应代币为同质化代币
发行代币。用户使用供应代币后按照曲线计算可以购买的另一种代币。发行代币可能是同质化代币,但也可以是非同质化代币,但非同质化代币的案例较少见
曲线。用于决定价格,有些应用仅使用一条曲线决定买入价格和卖出价格,而还有一些应用使用了更加复杂的机制,其买入和卖出价格遵循不同的曲线,两者的价差实际上就是交易的税收
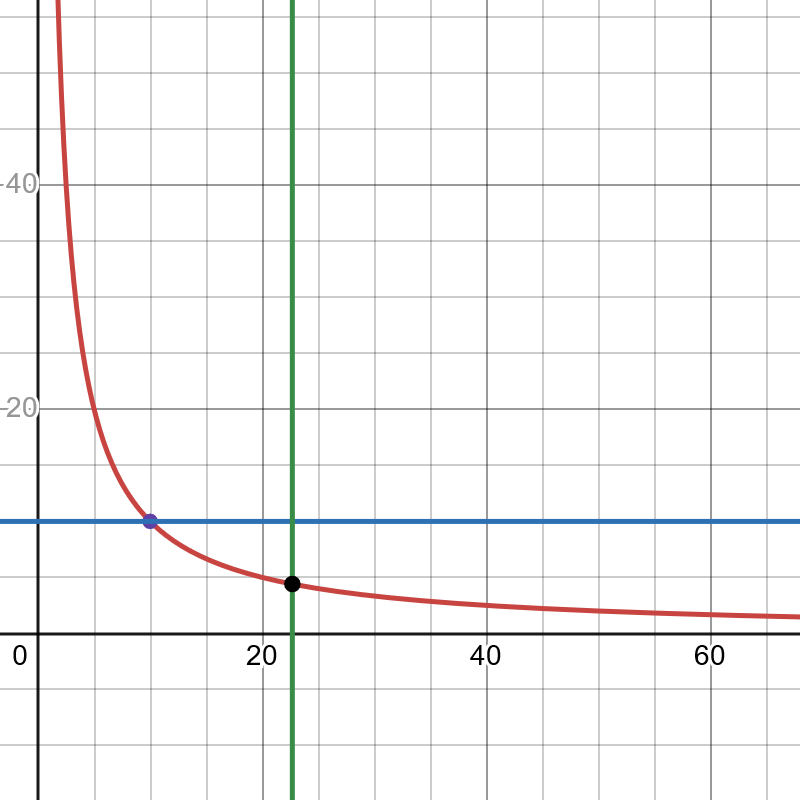
在 Bonding Curve 领域,最核心的就是曲线,因为曲线决定着用户买入和卖出的价格。最简单的曲线形式如下: $$ y=m \cdot x^n $$ 下图展示了 $y = \frac{1}{400}x^2$ 的图像:
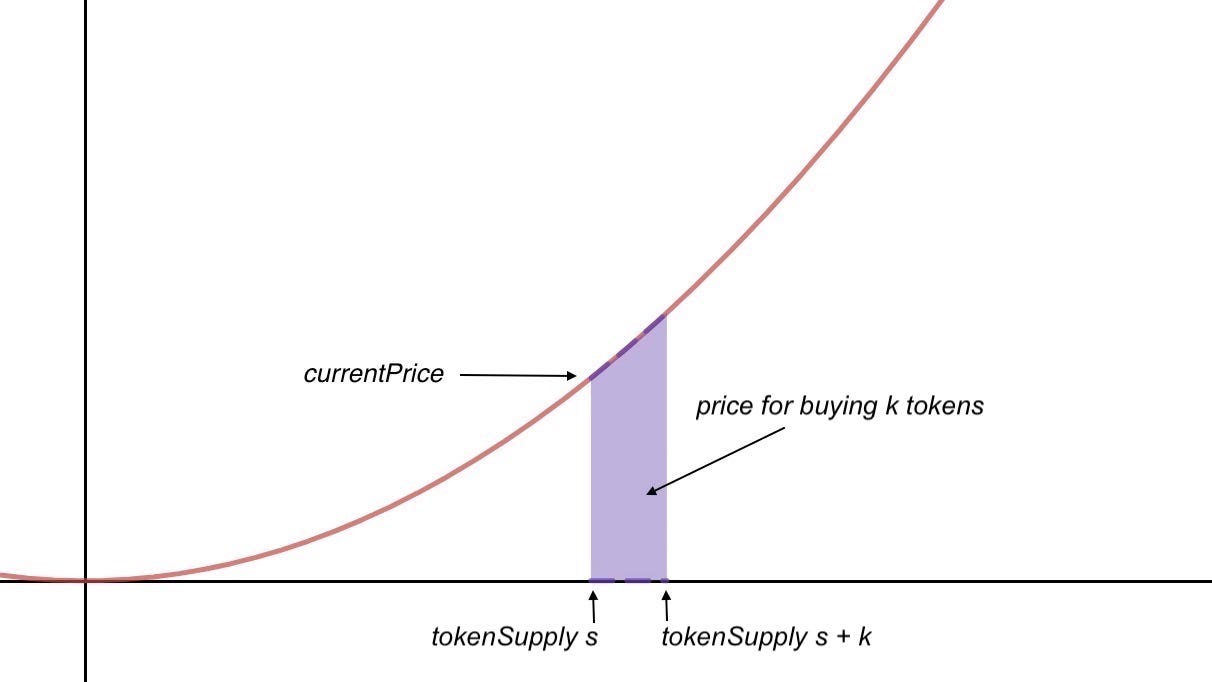
当用户决定进入市场时,假如用户需要购买 $k$ 数量的发行代币,我们会使用曲线下的积分计算用户所需要的供应代币的数量。当然,我们会使用一些方案简化积分计算。该过程涉及到一系列数学推导,如果读者对其感兴趣,请阅读 Bonding Curves In Depth: Intuition & Parametrization 一文中的 Computing Buy and Sell Prices 章节。
下图展示了一些常见的用于 Bonding Curve 的曲线。左上角为 Sigmoid 曲线,其曲线的函数表达为 $y = \frac{1}{1-e^{-x}}$,右上角为幂函数曲线,其函数表达式为 $y = m \cdot x^n$。左下角为特殊函数曲线,其数学表达式为 $y = m(1+25\%)^{log_2x}+b$,其经济学含义为当代币供应量每增加一倍,代币的价格就增加 25%。如果读者对此特殊函数十分感兴趣,请阅读 On Single Bonding Curves for Continuous Token Models 一文。而右下角为常数函数。

事实上,这些曲线都可以归结为亚线性、线性和超线性。
与 AMM 曲线方案相比,Bonding Curve 最大的优势在于完全不依赖于初始流动性,代币发行方并不需要准备大量流动性,而是可以直接进行代币发行,靠用户注入流动性来维护价格。这极其有利于所谓的策展市场(Curation Markets)。策展市场是早期以太坊的讨论议题之一,其目的是允许团体更有效地协调并从他们围绕共同目标共同创造的价值中获利的模型。最简单的案例就是目前的 pump.fun。策展人发行 MEME,其他参与者按照 Bonding Curve 买入发行的 Meme 代币。而 friend tech 也是策展市场的案例之一。
如果读者希望获得更加详细的信息,请参考 Introducing Curation Markets: Trade Popularity of Memes & Information (with code)! 一文,值得一提的是该文成文于 2017 年。
对于 Bonding Curve 而言,最大的问题在于过于机械的规则导致代币无法长时间运转。对于 FriendTech 等应用而言,使用曲线存在一部分问题,导致早期参与者可以在后期获得可观的涨幅,这种透明规则导致大量机器人早期参与然后后期直接选择退出导致中期参与者资产受损。对于 pump.fun 而言,也存在此问题,但是 pump.fun 创造性的只使用 Bonding Curve 作为早期 LP 筹资工具,而后期则直接使用 AMM 模型交易,这种方案一定程度上减少了机械式的曲线的影响。
拍卖
拍卖也是常见的定价方案,此定价方案适用于任何资产。由于技术问题,我们一般不在链上进行密封拍卖,一般来说,我们常使用以下两种拍卖方案:
- 荷兰式拍卖。目前链上使用最多的拍卖方式,标的资产从提前设置的最高价起拍,随着时间的推移,价格逐渐降低,直至成交
- 英式拍卖。在固定时间内,标的资产价格逐步推高,到拍卖结束时以最高价成交。
由于拍卖可以对任意资产进行比较合理的定价,所以目前以太坊内存在大量特殊生态使用了拍卖。比较常规的非连续英式拍卖在 flashbot 内经常使用,主要用于 MEV 机器人争夺交易位置:
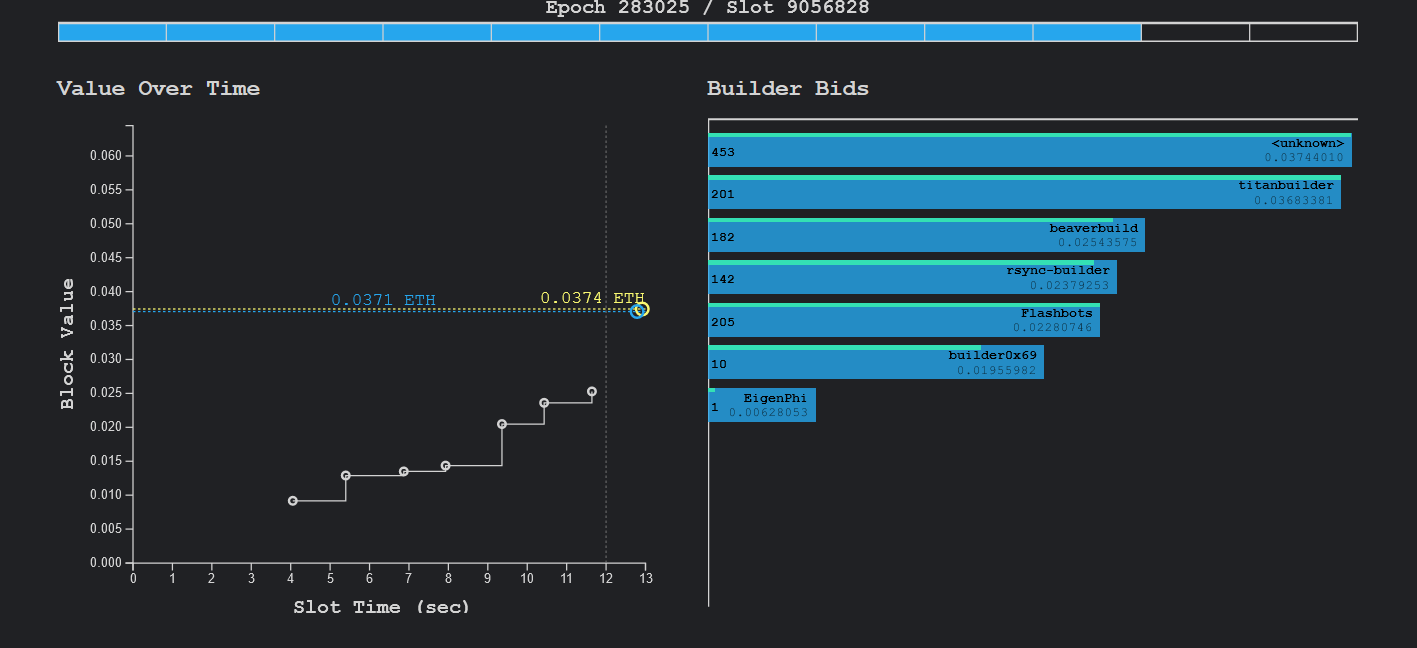
上图展示了不同的构建者争夺区块 MEV 机会的拍卖情况。读者可以在 payload.de 内实时看到任一区块内的 MEV 拍卖情况,上图就是截取自该网站。该拍卖使用了英式拍卖,即不同的参与者会逐渐给出更高价格以获得 MEV 机会。对于以太坊而言,FlashBot 的存在避免了 MEV 机器人发起 gas 战争,降低了以太坊的 gas 费用,而对于出块节点而言,可以进一步获取区块的 MEV 收益,使得其更加有利可图。由于效率问题,英式拍卖较少用于真正的以太坊资产发行。也有部分 Intent 系统使用了英式拍卖以最大化 Intent 发起人的效益,比如 CowSwap 在贷币兑换时就使用了英式拍卖。比如 Intent 发起人给出 100 个代币 A 可以兑换至少 80 个代币 B 的边界,其他的参与者可以给出多于 80 个代币 B 的报价。报价最高者可以获得 100 个代币 A 并给 Intent 发起人报价数量的代币 B。
荷兰式拍卖也是常用的拍卖方案之一,而且渐进式荷兰式拍卖(GDA) 被真正用于过资产发行。我们首先介绍非连续的荷兰式拍卖,这种拍卖一般较少用于资产发行,但有时会被用于资产的互换。UniswapX 允许用户提交荷兰式订单。假如用户希望将 100 个代币 A 兑换为 50 - 80 个代币 B,其可以向 UniswapX 提交荷兰式订单,该订单内包含 100 个代币 A,且要求获得的代币 B 的数量会随着时间从 80 开始衰减。假如目前衰减为 75 个代币 B,存在用户(在 UniswapX 内,我们称此用户为填单者 filler)接受此订单,该用户需要付出 75 个代币 B 就可以获得订单内 100 个代币 A。
而在于真正的资产发行场景内,我们一般使用 Paradigm 提出的渐进式荷兰式拍卖(GDA)和可变利率荷兰式拍卖(VRGDA)。渐进式荷兰式拍卖可以用于同质化和非同质化代币发行,其特点在于只需要一次启动就可以完成所有的代币发行,无需代币发行方手动启动每一次代币拍卖。其原理是在代币发行时,按照不同的起拍价一次性启动所有发行代币的拍卖。具体原理可以参考 深入探索 GDA 与 VRGDA 一文。
而可变利率荷兰式拍卖相比于 GDA 而言,附带了时间因素,其允许代币发行方设置代币释放曲线,当代币发行数量多于预期的代币发行曲线时,VRGDA 将提高价格以抑制需求;反之则降低价格以提高需求。
对于主要用于资产发行的 GDA 和 VRGDA 都存在一个严重的问题,用户参与拍卖时由于随着时间推动,资产的价格一定是降低的,大量用户在博弈过程中更倾向于等待以获得更低的价格。当所有用户都选择等待时,发行的资产价格会持续下降。事实上,我们可以将 GDA 和 VRGDA 看作 Bonding Curve 方案的变体,其并没有解决 Bonding Curve 的问题,反而丧失了 Bonding Curve 的二级市场功能。
而且 GDA 和 VRGDA 仅仅解决了一级市场的问题,而没有解决二级市场的问题,当资产拍卖结束后,代币发行方可以选择将拍卖过程中获得的资产放入 AMM 市场,但更有可能的是,代币发行方进行 soft rug,不再继续推动项目。对于拍卖参与者而言,拍卖所获得的资产并没有被赋予流动性,资产的定价也是相当不真实的。
ERC7527
ERC7527 是一个极其适合定价的资产发行方案,其解决了 Bonding Curve 方案的诸多弊端,并且保证了资产的流动性。ERC7527 的具体运作流程如下:
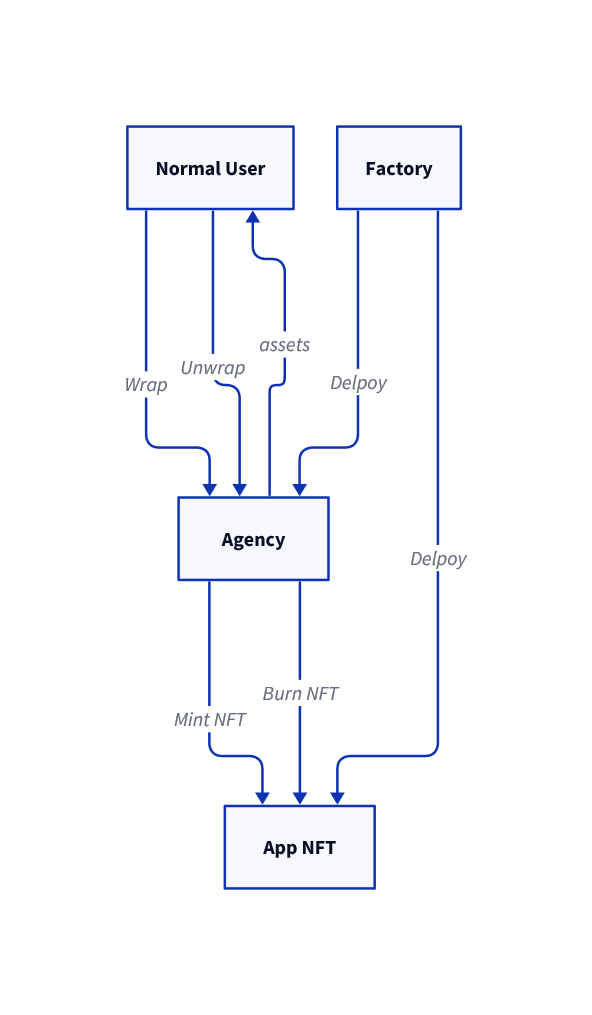
ERC7527 系统内包含以下三部分:
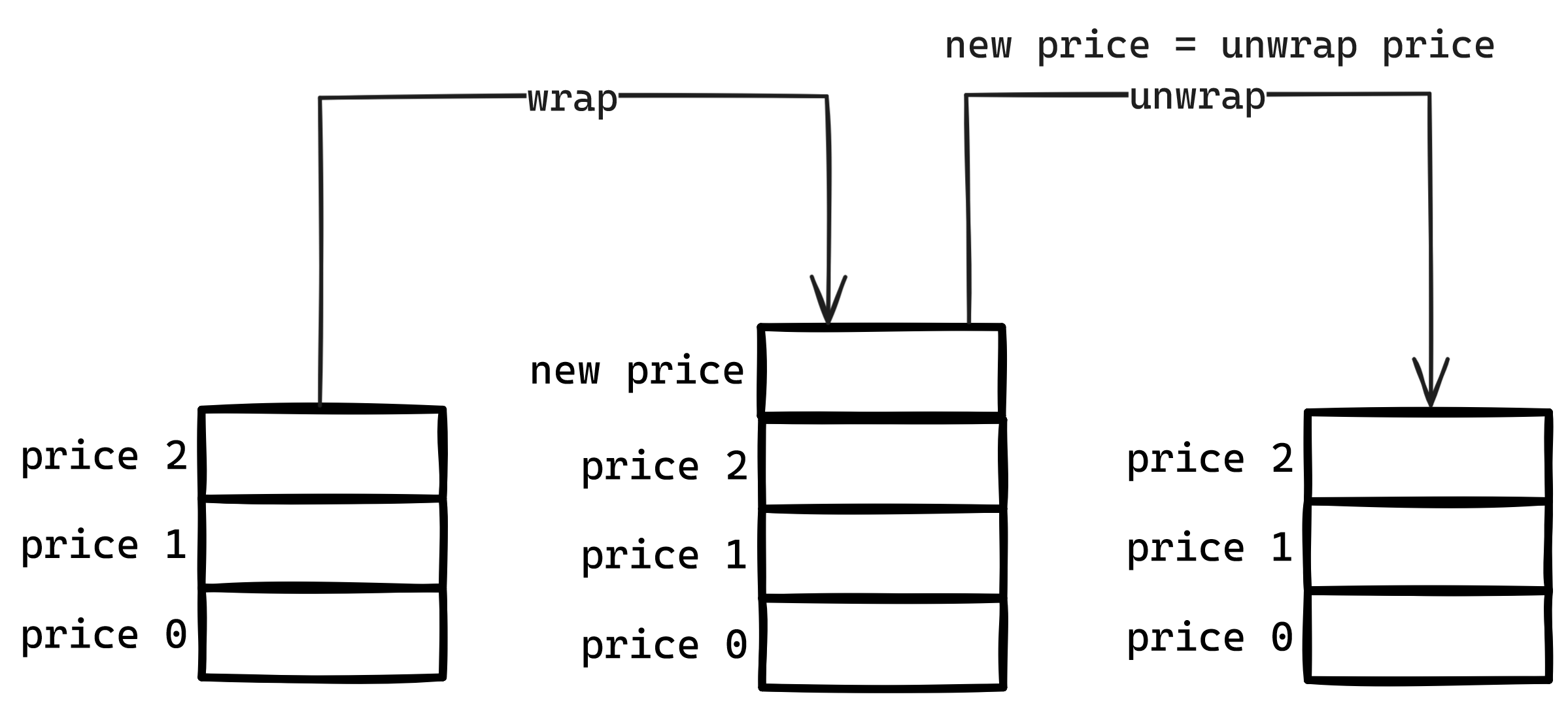
- Agency 用于储备资产的池,该池子会按照其内部函数对外不断给出买入报价和卖出,当用户接受买入报价时就可以将预先规定的资产存入 Agency,此时 Agency 会调用 App 的
mint函数为用户铸造 NFT,我们称此操作为wrap;当用户接受 Agency 的卖出报价,Agency 会将资产发送给用户并调用 App 的burn函数销毁,我们称此操作为unwrap - App 是一个继承 NFT 的资产类型,由于 Agency 的保证,该资产始终可以保持流动性
- Factory 方便用户部署 Agency 和 App。用户只需要输入部分参数即可直接部署 Agency 和 App
在这里存在一个核心问题,Agency 如何对外给出买入报价和卖出报价?一个最简单的方案是在 Agency 内部使用了类似 Bonding Curve 的方案,直接基于 NFT 的总供应量等直接计算获得报价。但这种方案仍没有解决 Bonding Curve 的问题。在此处,我们使用了一些更加有趣的函数,该函数的目标是将用户的买入行为纳入最终的报价结果。报价使用的具体函数依赖以下参数:
- $\Delta_m$ 用户此次铸造与上一用户成交的时间差
- $p_{n-1}$ 上一次成交的价格
- $p_n$ 本次成交的价格
基于上述参数,我们可以给出以下价格函数:
$$ p_n = \begin{cases} \frac{2}{1+e^{\lambda_{up} \Delta_{m}}} \cdot p_{n-1} + c & \Delta_m \le \Delta_{target} \\ p_{max}e^{-\lambda_{down} \Delta_{m}} &\Delta_m > \Delta_{target} \end{cases} $$ 此函数包含几个常量:
$c$ 当用户买入后,下一次报价与用户成交价的跳跃,避免在连续购买时报价上涨较低的情况
$\lambda_{up}$ 决定价格上涨速度,此数值必须小于 0,且绝对值越大代表上涨速度越快
$\lambda_{down}$ 决定价格下降的速度,此数值必须大于 0,且绝对值越大代表下降速度越快
$p_{max}$ 实际上指 $\Delta_m = \Delta_{target}$ 情况下的 $p_n$ 值,该值代表这个区间内的最大值
$\Delta_{target}$ 决定上升阶段的最长时间,用于与 $\lambda_{up}$ 和 $p_{max}$ 参数一同作用,决定最终的上涨幅度
在上述函数内,没有表达的是 $p_n$ 始终大于等于 $p_{n-1}$ 。即本次成交价不得低于上一次成交价。
下图显示了在一次区间内,Agency 给出的报价情况,下图给出的报价均为相对值,其纵坐标代表 $\frac{p_n}{p_{n-1}}$
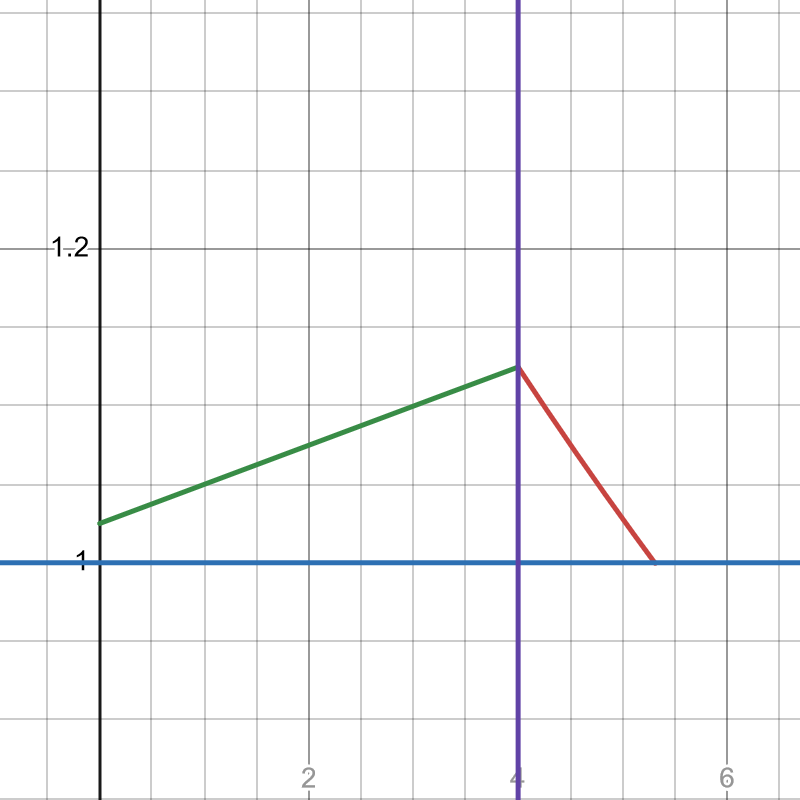
上文我们已经介绍了如何进行买入报价,但还没有介绍如何进行卖出报价。卖出报价实际上就是上一次的买入成交价。在合约内,我们会维护一个价格列表,每一次成家后都将成交价追加到价格列表后,而当用户卖出时,就直接使用价格列表的最后一个价格作为用户的卖出报价。在具体的价格表现上,就会出现用户的买入和卖出存在一定的对称性。
在引入以上 Agency 报价公式后,就可以避免 Bonding Curve 完全透明的价格曲线,所有的价格确定都是用户通过买入和卖出驱动的,所以用户不再仅与报价函数博弈,更多的是与其他用户进行博弈。比如用户不会仅选择等待策略,因为在报价上涨阶段就有可能出现成交。最终在动态博弈下会产生比 Bonding Curve 更加复杂的博弈场景。下图展示了随机模拟下的 App NFT 的成交价格情况:
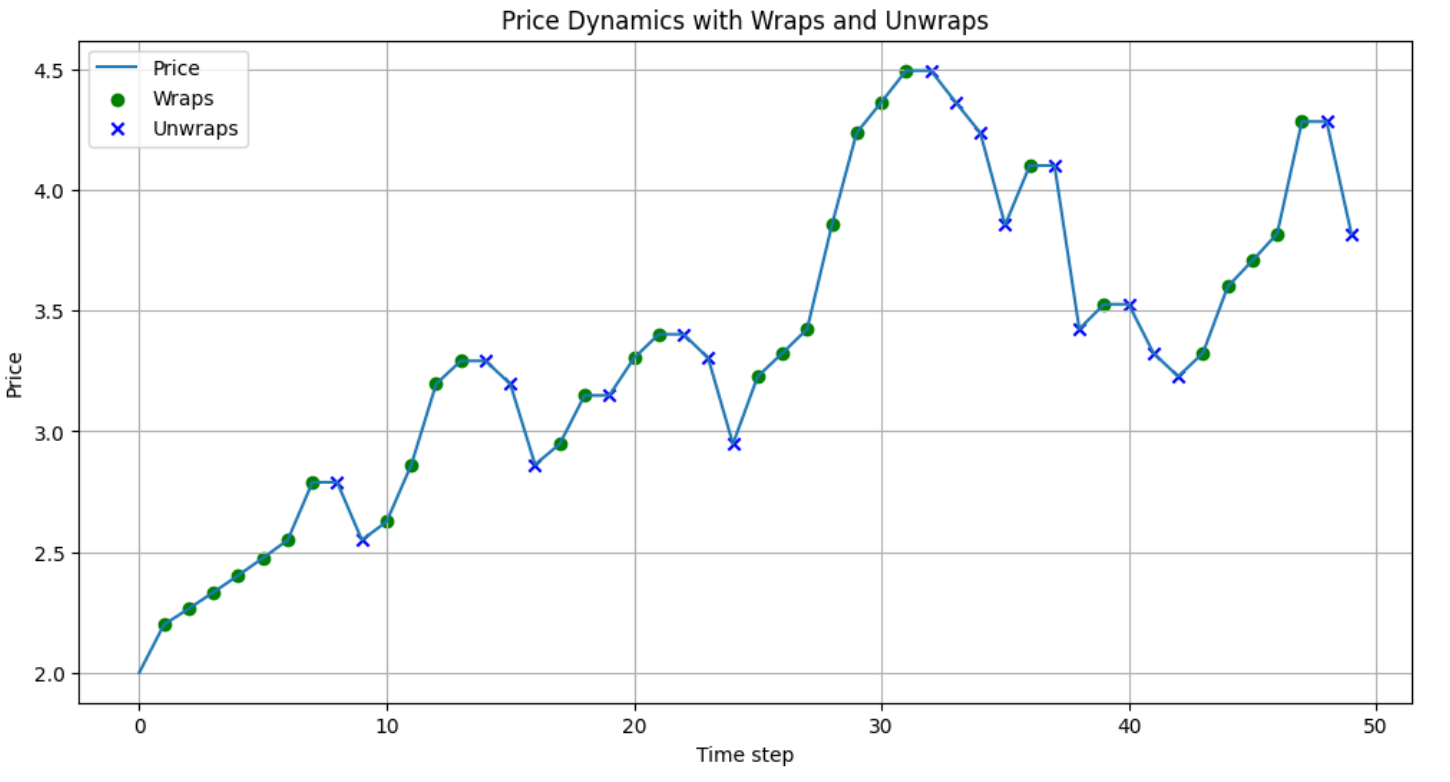
与 Bonding Curve 相比,我们可以将上述报价过程视为 Bonding Curve 与拍卖机制的结合,拍卖过程的博弈刚好弥补了 Bonding Curve 过于透明化的机制。但另一方面也保留了 Bonding Curve 的其他优势。用户通过 wrap 获取 App NFT 后,Agency 所代表叙事或者映射的实体就与其经济利益息息相关,基于经济利益的驱动,用户有可能参与 Agency 所对应的叙事或者实体的构建。而 Agency 的 TVL 也刚好反映了 Agency 所对应叙事的价值。比如用户可以选择使用 Agency 发行 Meme NFT。用户认可此 Meme 就会使用 wrap 操作用钱投票,并积极推动其他用户参与。而 Agency 的 TVL 则直接反映了当前 Meme 的市场价值。
与拍卖方案相比,ERC7527 方案的另一大优势在于资产具有充分的流动性,用户可以选择直接在二级市场内换手,如果二级市场流动性并不充足,那么用户可以选择直接通过 Agency 的 unwrap 机制销毁 NFT 获得底层资产。而且 Agency 内的资产并无法被代币发行方提取,一定程度上避免了代币发行方的 Rug 行为。
与 AMM 机制相比,ERC7527 也具有维护代币流动性的特点,但比 AMM 不同的一点在于,ERC7527 的流动性是自提供的,即参与 wrap 操作的用户注入的资金为整个 Agency 做市。相比于外部流动性提供方,这种流动性的自提供避免了很多问题,比如代币发行方并不需要提供初始流动性,而只需要等待用户 wrap 参与即可。而且更不需要参与者进行复杂的 LP 管理。由于价格是基于上述报价函数决定的,大部分情况下,流动性提供方并不会受到 MEV 攻击的影响。
总结
本文依次介绍了以下几种目前常用的纯链上定价模型:
- AMM 曲线。目前共识最强的链上定价范式,但仅能为 ERC20 代币提供定价,且在流动性提供方面存在一系列问题,比如初始流动性的来源困难、流动性提供方存在潜在的损失以及 MEV 问题
- Bonding Curve。早期较为广泛讨论的定价范式,理论上可以为任意资产定价,而且不存在流动性提供方面的问题。但是其博弈仅依赖于公开的数学函数,无法较长时间的运行,往往到后期就会走向死亡
- 拍卖方案。常用的定价方案,但无论英式拍卖还是荷兰式拍卖都无法解决后续的流动性问题,使用拍卖的代币发行方往往会一次性提取所有的拍卖所得
相比于上述方案,ERC7527 则综合了不同方案的优点。首先在 Bonding Curve 原有的范式内引入了拍卖机制,使得博弈更加动态,避免过于透明的机制导致的问题。其次,ERC7527 选择将用户所有注入的资产用于发行资产的做市,避免了发行资产的流动性问题,而且也规避了 AMM 曲线的流动性提供方面的一系列问题,特别是初始流动性的问题。最后,ERC7527 保留了所谓的策展市场的相关能力,参与 wrap 的用户实际上都是利益共同体,这些用户在经济利益的驱使下主动推动相关 Agency 的发展。