概述
对于伪随机数的生成,特别是正态分布随机数的生成在智能合约内拥有较为广阔的使用场景。本文主要讨论链上的伪随机数生成。链上没有真随机数的观点是正确的,但是此观点不应该阻碍智能合约工程师探索链上高质量伪随机数生成,链上也有具有较难操纵的随机数来源,比如 EIP-4399 引入的 PREVRANDAO 操作码,但是将此随机数作为种子计算如正态分布的随机数的有关讨论则较少在智能合约领域提及,本文主要对此问题进行讨论。
我们将按照以下顺序讲解本文内容:
- 均匀分布随机数生成
- 正态分布随机数生成
读者应当按照顺序阅读。如无特殊说明,本文给出的代码都是 python 编写。关于智能合约对随机数生成算法的实现,我们会在下一篇文章介绍。
本文在编写过程中主要参考了 计算机程序设计艺术 第二卷 半数值算法 ,但本文会给出相关算法的 Python 实现以及更加详细的分析。
值得注意的是,本文给出的随机数依旧是伪随机数仍可以被提前预测,使用前请读者认真评估经济安全性。在 ERC7527 内,本文给出的正态分布随机数仅用于 wrap 操作,即仅用于给出买入报价,而不用于给出卖出报价,在此场景下,正态分布随机数是具有经济安全性的,即使该随机数被预测仍可以保证系统内的资产不产生损失。
均匀分布随机数生成
我们希望生成一个数值位于 $[a, b]$ 区间内的随机数,要求随机数生成算法产生的随机数为此区间内的任一数字,且要求各数字被随机数算法产生的概率相同。
线性同余法
此算法要求我们首先选定四个常量 $m$ 、$a$ 、$c$ 和 $X_0$ 。此处的 $X_0$ 即为随机数算法的起始点,也可以认为是此随机数算法的种子(seed)。
我们基于以下算法计算序列中下一个随机数:
$$ X_{n+1} = (a X_n + c) \mod m $$
我们设置 $m = 10$ 和 $X_0 = a = c = 7$ ,编写以下函数:
m = 10
x = a = c = 7
def lehmer_random(x, m, a, c):
return (a * x + c) % m
for i in range(0, 20):
x = lehmer_random(x, m, a, c)
print(x, end=",")
输出如下:
6,9,0,7,6,9,0,7,6,9,0,7,6,9,0,7,6,9,0,7
此随机数序列以 7,6,9,0 组合循环。
对于 $X_{n+1}= f(X_{n})$ 函数生成的均匀分布随机数,一定会出现循环,证明如下:
根据匀分布随机数的定义,存在 $0 \le X_n < m$ 。如果我们生成了 $m+1$ 个不同的值,根据抽屉原理,存在 $i$ 和 $j$,其中 $i \neq j$ 且 $X_i = X_j$。如果 $X_i = X_j$,那么根据 $X_{n+1} = f(X_n)$,我们有 $X_{i+1} = f(X_i)$ 且 $X_{j+1} = f(X_j)$。由于 $X_i = X_j$,所以 $X_{i+1} = X_{j+1}$。
以上证明了序列 ${X_n}$ 在某一时刻开始重复,从而具有周期性循环。
接下来,我们希望寻找更好的线性同余计算公式的参数使得循环周期尽可能大。
模数 m 的选择
我们应当选择 $2^n$ 作为 $m$ 是一个较好的选择的,因为 $2^n$ 在进行模运算时具有快速算法,我们可以使用以下代码进行模运算:
m = 16
x = a = c = 7
def lehmer_xor_random(x, m, a, c):
return (a * x + c) & (m-1)
上述算法使用了 $x \bmod 2^n = x \& (2^n-1)$ 简化计算,在 EVM 内,& 计算仅消耗 3 gas,而 mod 计算则消耗 5 gas。
事实上,为了更好的随机性,我们应当选择 $m = 2^n + 1$ 且 $c = 0$,即使用 $(aX) \bmod (w+1)$ 生成随机序列,此处的 $w = 2^n$ 。
此处的 $n$ 是根据计算机架构确定的,如在 EVM 内,可以选择 $n = 256$ 。
我们可以使用以下方法简化计算,设 $aX = qw + r$,根据上文给出的算法,我们可以使用 & 快速 $aX \bmod w$ 的值,结果为 $r$。
此处的 $q,r$ 为整数,那么:
$$ \begin{align} aX &= qw + r &\mod (w + 1) \\ &= q(w + 1) + (r - q) &\mod (w + 1) \\ &= (r - q) &\mod (w + 1) \end{align} $$
此处,在上文中,我们已说明 $0 \le r < w$ ,且因为此处所有数字均为正整数,所以 $q > 0$,故 $r-q < w$,故最终结果为 $ r - q$ (在 $ r - q \ge 0$ 的条件下)或 ($r - q + (w + 1)$ 在 $r - q < 0$ 的情况下)。我们不准备模拟此算法,因为在 EVM 内直接调用 MOD 操作码的成本更加低廉。
我们在此处讨论一下,为什么使用 $2^n \pm 1$ 作为 $m$ 的数值而不是更容易计算的 $2^n$。这是因为如果使用 $m = 2^n$ 则会出现低位数字的随机性较低的特点:
设 $d$ 是 $m$ 的因子,使用 $Y_n = X_n \bmod d$ 可以计算获得 $X_n$ 的低位数字,可以证明 $Y_{n+1} = (aY_n+c) \bmod d$ 。此处希望获得 $X_n$ 的低四位数字,需要取 $d = 2^4$ ,则 $X_n$ 的低四位为 $Y_n = X_n \bmod 2^4$ ,显然,该序列循环周期较短。
显然,另一个 $m$ 的因子越少,其生成的序列随机性越高,故一种选择是直接选择最大的素因子,如 EVM 内使用 $2^{256}$ 内的最大素因子
乘数 a 的选择
由 $m,a,c,X_0$ 定义的线性同余序列存在周期 $m$ 要求以下条件:
$c$ 与 $m$ 互素
$b = a - 1$ 可以被 $m$ 的素因子 $p$ 的整除
如果 $m$ 是 4 的倍数,则 $b$ 也是 4 的倍数
关于上述条件的证明是较为复杂的,本文不在此处展示其完整的证明过程。读者可以在 此处 找到常见的参数设置。
MMIX 内使用了 $m = 2^{64}$, $a = 6364136223846793005$ 而 $c = 1442695040888963407$ 的参数,我们尝试验证该参数是否符合上述要求。
我们使用 sage 对上述条件进行验证:
sage: gcd(6364136223846793005, 1442695040888963407)
1
sage: N = 2 ** 64
sage: F = N.factor()
sage: F
2^64
使用 gcd 计算 $c$ 和 $m$ 的最小公因数,可以证明 $c$ 和 $m$ 存在互素的关系。对 $m$ 进行素因子分解,可以获得 $m$ 的唯一素因子为 $2$ ,显然 $b = a - 1$ 可以整除 2 ,而第三点的成立是显然的。
当然,正如上文所述,使用 $m = 2^{64}$ 会导致部分随机数的低位随机性不足,但是影响不大。
我们接下来考虑一种特殊情况,即 $c = 0$ 的情况,此时随机数生成公式如下:
$$ X_{n + 1} = a X_n \bmod m $$
此形式可以简化计算,使用此公式生成随机数需要对 $a$ 进行特殊选择,选择规则如下:
- $X_0$ 与 $m$ 互素
- $a$ 是一个模 $m$ 原根(Primitive root modulo m)
上述条件过于抽象,论文 Computationally easy, spectrally good multipliers for congruential pseudorandom number generators 给出了一系列经过验证的良好参数选择。读者可以在论文最后找到作者总结的表格,我们使用的是 MCG 系列表格,此处的 MCG 即指 $X_{n + 1} = a X_n \bmod m$ 形式,而 LCG 则指 $X_{n+1} = (a X_n + c) \mod m$ 形式。
当 $m = 2^{64}$ 时,良好的参数选择如下:
| Bits | a | $\lambda$ |
|---|---|---|
| 32 | 0xe817fb2d | $1.81$ |
| 33 | 0x1e85bbd25 | $3.82$ |
| 34 | 0x34edd34ad | $6.62$ |
| 48 | 0xbdcdbb079f8d | $9.7 \times 10^4$ |
| 64 | 0xf1357aea2e62a9c5 | $9.1 \times 10^9$ |
我们可以使用 Python 函数模拟随机函数的散步情况,代码如下:
import itertools
import pandas as pd
def mcg_random(seed):
while True:
seed = (0xf1357aea2e62a9c5 * seed) % 2 ** 64
yield seed
x = list(itertools.islice(mcg_random(42), 1000))
y = list(itertools.islice(mcg_random(43), 1000))
df = pd.DataFrame(list(zip(x, y)), columns =['x', 'y'])
df.plot(kind='scatter', x='x', y='y')
获得的图像如下:
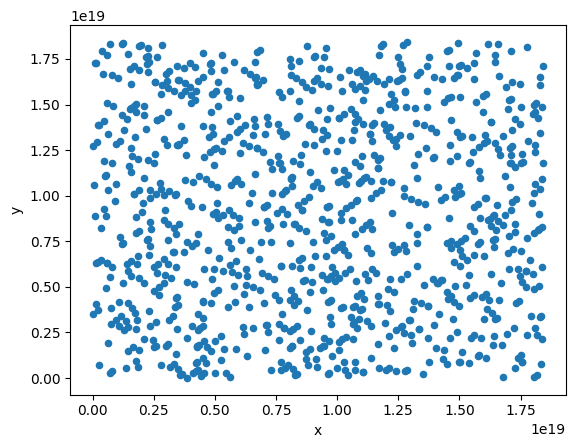
在本节的最后,我们讨论如何获得指定数据的模 $m$ 原根的 $a$。根据《计算机程序设计艺术 卷2:半数值算法》给出的算法,我们可以使用以下方法计算:
对于 $m - 1$ 的任意素因子,$a^{(p - 1) / m} \neq 1 \bmod p$
上述方程是无法通过解析方法求解的,我们一般直接使用遍历求解,代码如下:
from sympy.ntheory import factorint
from sympy import primerange
def find_primitive_root(start, m):
factors = factorint(m - 1) # Factorize m - 1
for a in primerange(start, m): # Iterate over potential candidates for 'a'
if all(pow(a, (m - 1) // p, m) != 1 for p in factors):
return a # Found a primitive root
return None
经验证明,当 $a \ge \sqrt{m}$ 时,获得的 $a$ 值较好,即此处的 start = int(mp.sqrt(m)) 时,获得的 $a$ 值较好。下文展示了当 $m = 2^{256} - 1$ 时,$a$ 的取值情况:
from sympy.ntheory import isprime
from mpmath import mp
m = 2 ** 256 - 1
while not isprime(m):
m -= 1
start = int(mp.sqrt(m))
print("m", hex(m))
a = find_primitive_root(start, m)
print("a", hex(a))
assert isprime(a)
基于哈希算法的随机数生成
keccak256(即 SHA3) 算法产生的随机值是等概率的,所以使用哈希函数作为等概率随机数生成器是有价值的,在 solady LibPRNG 中,我们可以看到如下代码:
/// @dev Seeds the `prng` with `state`.
function seed(PRNG memory prng, uint256 state) internal pure {
/// @solidity memory-safe-assembly
assembly {
mstore(prng, state)
}
}
/// @dev Returns the next pseudorandom uint256.
/// All bits of the returned uint256 pass the NIST Statistical Test Suite.
function next(PRNG memory prng) internal pure returns (uint256 result) {
// We simply use `keccak256` for a great balance between
// runtime gas costs, bytecode size, and statistical properties.
//
// A high-quality LCG with a 32-byte state
// is only about 30% more gas efficient during runtime,
// but requires a 32-byte multiplier, which can cause bytecode bloat
// when this function is inlined.
//
// Using this method is about 2x more efficient than
// `nextRandomness = uint256(keccak256(abi.encode(randomness)))`.
/// @solidity memory-safe-assembly
assembly {
result := keccak256(prng, 0x20)
mstore(prng, result)
}
}
展示了如何使用 keccak256 产生可靠的随机数值。
正态随机数生成
在上文中,我们讨论了如何获得均匀分布的随机数,或称如何获得等概率分布的随机数。在本文中,我们将进一步讨论如何在等概率随机数基础上获得正态分布的随机数。
在介绍正态分布随机数生成算法前,我们首先引入 Irwin-Hall 分布 。该分布是有多个独立的等概率分布的随机变量的总和,其定义如下:
$$ X = \sum_{k=1}^{n} U_k $$
由于 中心极限定理 的存在,我们可以使用 Irwin-Hall 分布近似拟合正态分布。
中心极限定理告诉我们,大量随机变量之和近似服从正态分布的条件。
为了获得正态分布的变量,我们需要进行以下两个步骤:
- 使用均匀分布随机数生成器获取 20 个均匀分布的随机数
- 计算 20 个均匀分布随机数的总和
- 进行调整获得正态分布随机数
我们首先需要获取 20 个均匀分布的随机数我们可以通过上文介绍的均匀分布随机数生成器直接生成 20 个随机数,但是这样会消耗较多 gas。另一个选择是生成 uint256 范围内的随机数,然后将 uint256 随机数拆分为 4 个 uint64 随机数。使用这种方法,我们只需要生成 5 个随机数即可。
我们首先使用哈希算法生成第一个随机数,并使用该随机数作为种子基于 MCG 生成其他 4 个随机数,如下:
result := keccak256(prng, 0x20)
mstore(prng, result)
let n := 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff43
let a := 0x100000000000000000000000000000051
let m := 0x1fffffffffffffff1fffffffffffffff1fffffffffffffff1fffffffffffffff
let s := 0x1000000000000000100000000000000010000000000000001
let r1 := mulmod(result, a, n)
let r2 := mulmod(r1, a, n)
let r3 := mulmod(r2, a, n)
此处的 result 就是使用哈希算法获取的第一个随机数,同时也作为后期 MCG 的种子。此处,我们需要注意 MCG 的参数选择,其 n 值选择了一个 uint256 内的一个较大的素数。关于此处参数选择背后的具体代码,请参考 此代码
此处的
m作为掩码存在,用于将一个uint256随机数拆分为 4 个随机数。而s的作用较为特殊,我们会在下文详细介绍
当获取到 result 和 r1 等随机数后,我们接下来需要计算随机数的和,此处我们会使用一种高效算法。
我们以 r2 + r3 为例介绍如何高效计算随机数之和。我们首先需要使用 r2 & m 和 r3 & m 将 r2 和 r3 拆分为 4 个随机数,其每一个随机数之间使用 0 连接。
设 r2 = 0x37644e72e232a729b85445b68181585d2833e84879b9749943eef593f92574f5,其与 m 进行 & 计算后结果为:
0x 17644e72e232a729 185445b68181585d 0833e84879b97499 03eef593f92574f5
我们可以看到 r2 相当于被拆分为了 4 个随机数,每一个随机数都为 61 bit,且符合以下关系:
$$ r2 \And m = u^{r2}_1 \times 2^{192} + u^{r2}_2 \times 2^{128} + u^{r2}_3 \times 2^{64} + u^{r2}_4 $$
而 r3 & m 也符合以下关系:
$$ r3 \And m = u^{r3}_1 \times 2^{192} + u^{r3}_2 \times 2^{128} + u^{r3}_3 \times 2^{64} + u^{r3}_4 $$
此时我们的目标是计算以下式子的值:
$$ u^{r2}_1 + u^{r2}_2 + u^{r2}_3 + u^{r2}_4 + u^{r3}_1 + u^{r3}_2 + u^{r3}_3 + u^{r3}_4 $$
我们首先直接进行 r2 + r3 操作,我们记 $u^{r2}_1 + u^{r3}_1 = u_1$ ,其以此类推,获得如下结果:
$$ r2 + r3 = u_1 \times 2^{192} + u_2 \times 2^{128} + u_3 \times 2^{64} + u_4 $$
此处,我们可以引入另一个参数 s = 0x1000000000000000100000000000000010000000000000001,使用数学表达如下:
$$ s = 2^{192} + 2^{128} + 2^{64} + 1 $$
此时,我们可以进行以下操作:
$$ \begin{split} s &\times (r2 + r3) \\ &= (2^{192} + 2^{128} + 2^{64} + 1) \times (u_1 \times 2^{192} + u_2 \times 2^{128} + u_3 \times 2^{64} + u_4) \\ &= u_1 \times 2^{384} \\ &\phantom{=} + (u_1 + u_2) \times 2^{320} \\ &\phantom{=} + (u_1 + u_2 + u_3) \times 2^{256} \\ &\phantom{=} + (u_1 + u_2 + u_3 + u_4) \times 2^{192} \\ &\phantom{=} + (u_2 + u_3 + u_4) \times 2^{128} \\ &\phantom{=} + (u_3 + u_4) \times 2^{64} \\ &\phantom{=} + u_4 \end{split} $$
我们只需要最终将结果左移 192 位就可以获得需要的加法结果。上述计算使用 yul 的代码表示如下:
shr(
192,
mul(s, add(and(m, r2), and(m, r3)))
)
基于上述知识,读者应当可以理解以下代码中的 shr 和 add 部分:
result :=
sub(
sar(
96,
mul(
26614938895861601847173011183,
add(
add(
shr(
192,
mul(s, add(and(m, result), and(m, r1)))
),
shr(
192,
mul(s, add(and(m, r2), and(m, r3))))
),
shr(
192,
mul(s, and(m, mulmod(r3, a, n))))
)
)
),
7745966692414833770
)
我们可以将上述代码简化为:
result =
sub(
sar(
96,
mul(
26614938895861601847173011183,
sum
)
),
7745966692414833770
)
此处的 sum 即为计算获得的 20 个取样随机数的总和。此处的 20 个随机数的和符合均值 $\mu = n / 2$ 和方差 $\sigma ^{2}=n/12$ 的规则,此处的 $n = 20$。我们需要将其转化为标准正态分布,方法如下:
$$ z = \frac{X - \mu}{\sigma} = X \times \frac{1}{\sigma} - \frac{\mu}{\sigma} $$
有了上述公式,我们可以计算不同的参数。首先计算 $\frac{1}{\sigma}$ 的值,此处我们需要处理大量的精度问题。首先,为了提高精度,我们希望除法可以在 $10^{18} \times 2^{96}$ 范围内进行,而此处的 sum 为 $2^{61}$ 精度,我们需要进行如下计算获取 $\frac{1}{\sigma}$ 的精度调整值:
$$ \frac{1}{\sigma} = \frac{\sqrt{\frac{3}{5}} \times 2^{96} \times 10^{18}}{2^{61}} $$
上述计算结果为 26614938895861601847173011183。具体计算的 Python 代码如下:
from mpmath import mp
mp.prec = 1024
(mp.sqrt(mp.mpf(3) / mp.mpf(5)) * mp.mpf(2 ** 96) * 1e18) / mp.mpf(2 ** 61)
此处获得的 mul(26614938895861601847173011183, sum) 的结果精度为 $2^{96} \times 10^{18}$ ,我们可以使用右移 96 位的方式使其精度修正为 $10^{18}$
而 $\frac{\mu}{\sigma}$ 的计算也需要进行精度调整如下:
$$ \frac{\mu}{\sigma} = \frac{10}{\sqrt{\frac{5}{3}}} \times 10^{18} $$
我们可以使用以下代码计算:
10 / mp.sqrt(mp.mpf(5) / mp.mpf(3)) * 1e18
结果为 7745966692414833770
在本节的最后,我们介绍如何判断上述生成的正态分布随机数是符合标准正态分布的,我们首先将正态分布生成的 solidity 代码重写到 Python 中,如下:
import random
UINT256_MAX = 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
WAD = 1000000000000000000
def _add(a, b):
return (a + b) & UINT256_MAX
def _and(a, b):
return (a & b) & UINT256_MAX
def _mul(a, b):
return (a * b) & UINT256_MAX
def _mulmod(a, b, d):
return ((a * b) % d) & UINT256_MAX
def _shr(s, x):
return (x >> s) & UINT256_MAX
def _sar(s, x):
if x < 0:
return -_shr(s, -x)
return _shr(s, x)
def _shl(s, x):
return (x << s) & UINT256_MAX
def _sub(a, b):
return a - b
def generate():
n = 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff43
a = 0x100000000000000000000000000000051
m = 0x1fffffffffffffff1fffffffffffffff1fffffffffffffff1fffffffffffffff
s = 0x1000000000000000100000000000000010000000000000001
r = random.randint(0, UINT256_MAX)
r1 = _mulmod(r, a, n)
r2 = _mulmod(r1, a, n)
r3 = _mulmod(r2, a, n)
result = _sub(_sar(96, _mul(26614938895861601847173011183,
_add(_add(_shr(192, _mul(s, _add(_and(m, r), _and(m, r1)))),
_shr(192, _mul(s, _add(_and(m, r2), _and(m, r3))))),
_shr(192, _mul(_and(m, _mulmod(r3, a, n)), s))))),
7745966692414833770)
return result
def samples() :
n = 200000
# return np.random.standard_normal(n)
a = []
for i in range(n):
a.append(generate() / WAD)
return a
上述代码使用了 r = random.randint(0, UINT256_MAX) 来代替基于随机数种子哈希的均匀随机数生成。
接下来,我们需要使用 Kolmogorov-Smirnov test 判断上述函数 samples 生成的随机数序列是否符合正态分布。
Kolmogorov-Smirnov test 是一种验证样本是否来自某种概率分布的检验方法,该测试的原假设为样本 不 来自某种概率分布。
我们可以直接使用以下代码检验:
from scipy.stats import kstest
# Kolmogorov-Smirnov test.
kstest(samples(), 'norm')
输出如下:
KstestResult(statistic=0.0022907221160571867, pvalue=0.2443439536648484)
此处的 pvalue > 0.05,所以我们拒绝 samples() 函数结果不来自正态分布的原假设,认为 samples() 函数生成的结果是符合正态分布的。
总结
本文首先介绍了均匀分布随机数的生成算法,该部分内容主要参考了 《计算机程序设计艺术 第二卷 半数值算法》 一文,主要介绍了 MCG 生成方法及其参数计算方法。然后,基于均匀分布随机数的生成算法和 Irwin-Hall 分布,我们实现了正态分布随机数生成。此处主要介绍了 solady 代码中的相关函数。