概述
在 Uniswap V4 内,我们可以看到一些复杂的数学计算模块,这些数学计算相关的模块大部分都使用了内联汇编实现,同时包含了大量的 magic number。在本文,我们将详细分析数学计算模块的实现。
BitMath
在 src/libraries/BitMath.sol 文件内,Uniswap V4 实现了两个函数,注意这两个函数都是用于检索 uint256 中的 1 的索引位置。一般来说,我们定义 uint256 最左侧为索引值 0,而最右侧为索引值 255。
在 Uniswap V4 内,我们可以看到 mostSignificantBit 和 leastSignificantBit 两个函数。其中 mostSignificantBit 是用来搜索 uint256 内索引值最大的 1 所在的位置,或称搜索最高有效位的索引。而 leastSignificantBit 则用于检索 uint256 内索引值最小的 1 所在的位置,或称搜索最低有效位的索引。以 0b1111 为例,当我们调用 mostSignificantBit(0b1111) 返回结果为 3(索引值从 0 开始),而 leastSignificantBit(0b1111) 的返回值为 0。
在进行后文的介绍之前,我们需要进行一个简单的 Python 项目配置。在此处,笔者使用了目前最优秀的 Python 环境管理工具 uv。读者可以自行从 官网 进行安装。安装完成后,我们可以使用以下命令初始化项目:
mkdir math-solver
uv init
uv add z3-solver
此处我们为什么需要在项目内部增加一个 z3-solver 包?这是因为我们需要使用 z3 进行一些 magic number 的求解。
另外,值得一提的是,BitMath 内部的代码实际上都不是由 Uniswap V4 官方开发者编写的,代码都是在 solady 内部复制的。solady 是目前 gas 最优化的 solidity 合约库,内部包含大量极致的 gas 优化手段,如果读者侧重研究 gas 优化,solady 是必读的库之一。
注意,可能有读者会尝试将本文的技巧用于常规架构下编程工作,请谨慎考虑,因为现代 x86-64 CPU 架构往往提供指令直接实现,这些指令都是硬件层面实现的,效率远远高于本文给出的软件方案。如果读者有在常规架构下编程的需要,请自行阅读 BitScan Wiki 内的内容。
mostSignificantBit
我们首先直接给出 mostSignificantBit 的代码定义:
/// @notice Returns the index of the most significant bit of the number,
/// where the least significant bit is at index 0 and the most significant bit is at index 255
/// @param x the value for which to compute the most significant bit, must be greater than 0
/// @return r the index of the most significant bit
function mostSignificantBit(uint256 x) internal pure returns (uint8 r) {
require(x > 0);
assembly ("memory-safe") {
r := shl(7, lt(0xffffffffffffffffffffffffffffffff, x))
r := or(r, shl(6, lt(0xffffffffffffffff, shr(r, x))))
r := or(r, shl(5, lt(0xffffffff, shr(r, x))))
r := or(r, shl(4, lt(0xffff, shr(r, x))))
r := or(r, shl(3, lt(0xff, shr(r, x))))
// forgefmt: disable-next-item
r := or(r, byte(and(0x1f, shr(shr(r, x), 0x8421084210842108cc6318c6db6d54be)),
0x0706060506020500060203020504000106050205030304010505030400000000))
}
}
看上去上述代码似乎就是魔法,尤其是最后的 magic number,即 0x8421084210842108cc6318c6db6d54be 和 0x0706060506020500060203020504000106050205030304010505030400000000 看上去不在常人的认知范围内。
我们首先明确该函数的目的,该函数的目的是寻找最高有效位的索引。索引值的取值范围为 [0, 255],刚好可以使用 uint8 表示。举例说明,假如 x = 0x1f00a4,那么我们返回的结果是:
111110000000010100100
^
|
index
我们需要返回 0x1f00a4 = 0b111110000000010100100 内,最头部的 1 所处的索引。此处应该为 20。再次注意,索引从 0 开始。当我们需要在 256 位内搜索具有最大索引值的 1 时,我们应该会优先考虑到二分搜索。
在计算机科学中,
mostSignificantBit也被称为msb算法,
我们首先判断 x 是否比 0xffffffffffffffffffffffffffffffff 大。0xffffffffffffffffffffffffffffffff 实际上是 128 位 1 构成的。假如 x > 0xffffffffffffffffffffffffffffffff ,那么我们可以断定最头部的 1 位于 [128, 255] 的区间内部。此时,我们可以认为 r 应该是 0b1xxxxxxx 的形式,此处的 x 表示目前无法确认到底是 0 还是 1。更加精确的表达为我们现在可以确认 r 的最高位是 1,而 r 位于 [0, 6] 索引处的位无法确定数值。以上论述可以转化为以下代码:
r := shl(7, lt(0xffffffffffffffffffffffffffffffff, x))
按预期,我们应该进一步计算 r 的第 6 位的数值,我们首先可以使用 shr 右移输入 x。然后使用 lt 计算即可,确定 r 第 6 位数值的代码如下:
r := or(r, shl(6, lt(0xffffffffffffffff, shr(r, x))))
如果读者感觉上述描述较为抽象,那么可以考虑自己使用纸和笔画图理解,下图展示假如最大索引值 1 较大情况下的经过两次二分的结果:
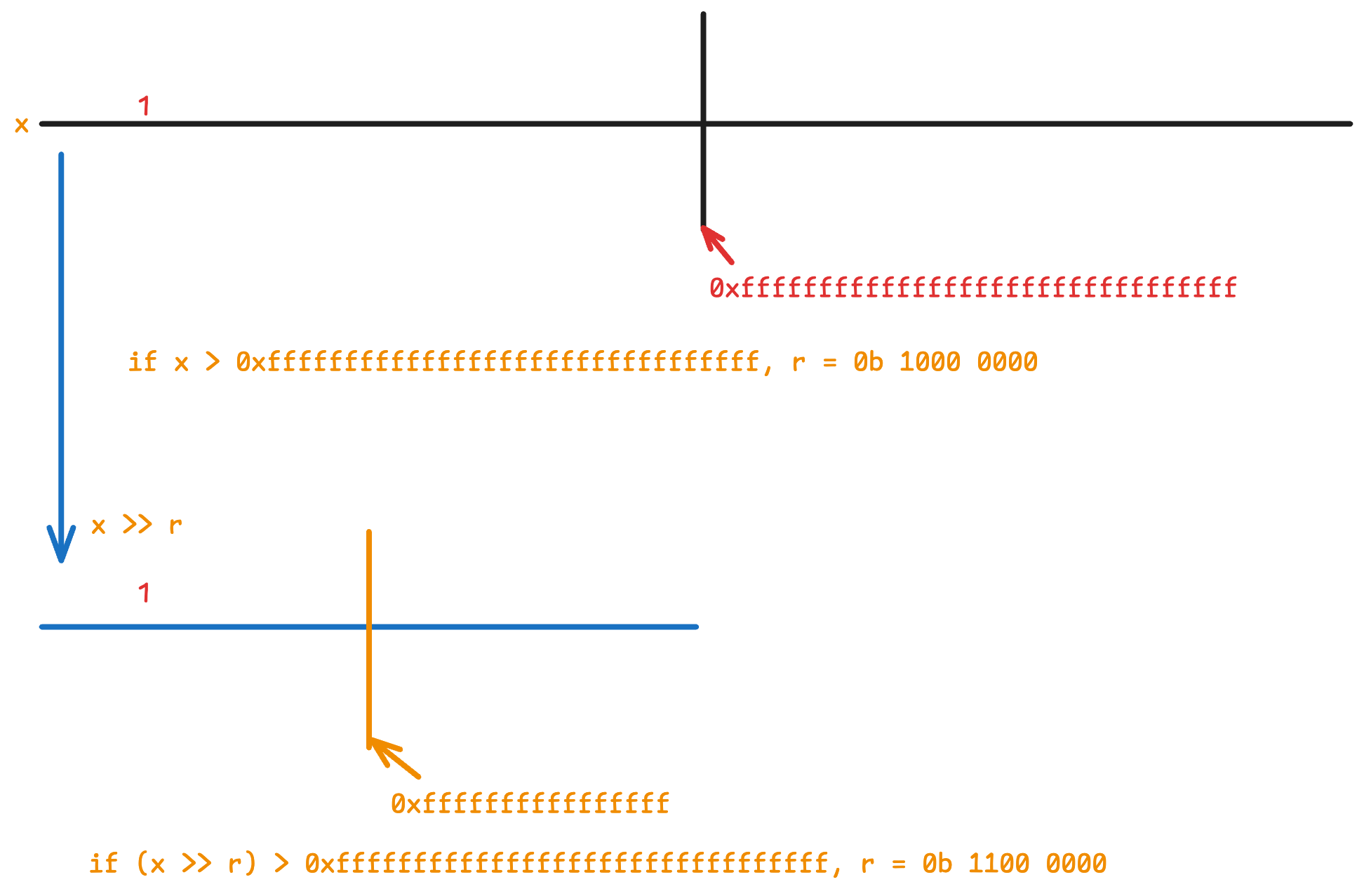
所以,经过 5 次二分后,我们可以确定 r 的 [3, 7] 的数值情况,但我们仍不知道 [0, 2] 的情况,即我们面前知道 r 的最低的三位的数值。
r := shl(7, lt(0xffffffffffffffffffffffffffffffff, x))
r := or(r, shl(6, lt(0xffffffffffffffff, shr(r, x))))
r := or(r, shl(5, lt(0xffffffff, shr(r, x))))
r := or(r, shl(4, lt(0xffff, shr(r, x))))
r := or(r, shl(3, lt(0xff, shr(r, x))))
一种较为简单且朴素的方法是在进行三次二分,就可以完成 r 所有数值的确认。但此时我们可以转变思路,可以尝试使用查表的方法。考虑到,假如此时计算 shr(r, x) 的结果只有 8 位长度。我们可以简单计算一下 8 位长度下,共有多少种可能性?
shr(r, x) = 0b 1111 1111 -> r[2-0] = 0b111
shr(r, x) = 0b 0111 1111 -> r[2-0] = 0b110
shr(r, x) = 0b 0011 1111 -> r[2-0] = 0b101
...
简单计算就可以知道 shr(r, x) 共有 256 种可能存在组合,这 256 种不同的组合对应有不同的 r[2 - 0]。此处的 r[2 - 0] 是指 r 的低三位数值。我们是否可以尝试利用位移和查表(具体表现为 byte) 求解 r[2 - 0]。
从思路讲,我们实际上希望获得一种特殊类型的映射计算 $f$,实现 $f(0b 1111 1111) = 0b111$ 的效果。众所周知,哈希算法往往存在类似效果,而构建哈希算法往往使用位移和查表。
按照上述说法,我们的目标是计算 lookup(q >> shr(r, x), l) = msb(shr(r, x)),此处的 msb 就是指 mostSignificantBit 算法。而 q 是一个常数用于计算最终的索引,而计算出的索引直接在 l 内进行检索。检索过程中,我们会使用 lookup 函数,该函数允许我们使用索引值在 l 内检索某些二进制数据。为了方便在 EVM 内实现,我们此处直接使用 byte 操作码作为 lookup 函数。byte 操作码允许我们从一个 uint256 内按索引获取 8 个二进制。
我们会发现 shr(r, x) 的所有 256 种取值,实际上就是指 shr(r, x) 的取值范围为 [0, 256]。那么输入已知,所需要的函数已知,但是函数使用的常数未知,这种情况下,我们就可以使用 z3 求解工具。代码如下:
from z3 import BitVec
from z3 import solve
l = BitVec('l', 256)
q = BitVec('q', 256)
byte_lookup = lambda i, x: (x >> ((31 - (i & 31)) << 3)) & 0xff
solve(
*[byte_lookup(q >> i, l) == len(bin(i)) - 3 for i in range(256)],
q >> 128 == 0,
l & 0xffffffff == 0,
)
我们最初声明 l 和 q 都是 256 位二进制数据。而 byte_lookup 实际上是直接根据的 byte 在 execution-specs 内的实现改编的。
当然,实际上更有可能是直接从 smol-evm 内复制的。
@insn(0x1A) def BYTE(ctx: ExecutionContext) -> None: offset, value = ctx.stack.pop(), ctx.stack.pop() if offset < 32: ctx.stack.push((value >> ((31 - offset) * 8)) & 0xFF) else: ctx.stack.push(0)
然后,我们直接使用 byte_lookup((q >> i) & 0x1f, l) == len(bin(i)) - 3 对所有的 256 种情况进行遍历计算。此处使用了技巧,即在 [0, 255] 的区间内, len(bin(i)) - 3 实际上等同于 msb 算法,这是因为 Python 中的 bin 函数不会对结果进行 0 填充处理。
剩下的 q >> 128 == 0 和 l & 0xffffffff == 0 都是一些特殊的限制条件,理论上没有也可以,这些限制条件来增加 q 和 l 的输出情况,核心目的是增加 q 和 l 内 0 的数量,因为在 EVM 内,0 比 1 更节省 gas。
我们将以上给出的 python 代码保存在 math-solver 目录下的 solve.py 中,然后执行 uv run solve.py 就可以获得以下输出:
[l = 3176832568382053665962636707163332082829746493830894041356796818399745277952,
q = 175629608733387594055148477185495225533]
此处读者获得的输出可能与我的输出不一致,这是因为我们给定的上述限制条件内,q 和 l 存在多个解。在 solady 版本内,开发者实际上是使用了以下参数:
l = 3176832568382053640854229765616608417700587278678501850580078522814972297216
q = 175629608733387594055579892975202555070
我们可以使用以下代码验证上述解是否符合我们的求解条件:
from z3 import BitVec
from z3 import solve
l = BitVec('l', 256)
q = BitVec('q', 256)
byte_lookup = lambda i, x: (x >> ((31 - (i & 31)) << 3)) & 0xff
solve(
*[byte_lookup(q >> i, l) == len(bin(i)) - 3 for i in range(256)],
# q >> 128 == 0,
q == 175629608733387594055579892975202555070,
l & 0xffffffff == 0,
)
我们可以看到求解获得 l = 3176832568382053640854229765616608417700587278678501850580078522814972297216 是符合预期的。
简单来说,当读者求解完成上述常数后,就可以完成 r 最低三位的计算工作,我们使用 solady 计算获得的结果:
r := or(r, byte(and(0x1f, shr(shr(r, x), 0x8421084210842108cc6318c6db6d54be)),
0x0706060506020500060203020504000106050205030304010505030400000000))
此处存在一个 and(0x1f, shr(shr(r, x), 0x8421084210842108cc6318c6db6d54be)) 内出现了 and 操作,在上文内,该操作并没有出现,这是因为 and 操作可以规范 shr(shr(r, x), 0x8421084210842108cc6318c6db6d54be) 输出的取值区间,避免获得大于 byte 条件的索引值。这是一种防御性编程的方案,实际上在 solady 内大部分使用 byte 的地方都使用了 and(0x1f, i) 类型的代码规范索引值。
至此,我们就完成了 msb 算法的介绍。在此处,我们介绍一下 msb 算法的其他几个名称:
fls算法(Find last set)log2算法,即用于计算某一个整数的log2数值
msb 算法也可以转化为前导零计数算法。因为我们已经知道最高位 1 所在的位置,使用 256 - msb(x) 就可以获得 x 的高位存在 0 的数量。前导零计算算法也有多个名称:
nlz算法(number of leading zeros)clz算法(number of leading zeros)
在 Huff实战:编写测试极致效率数学模块 我们曾介绍过前导零计数的一个复杂版本。当然,在 solady 内,为了节省 gas,solady 单独实现了 clz 算法。
leastSignificantBit
leastSignificantBit 是一个用于寻找当前最低位的 1 索引值的函数,或者更加权威的说法是 leastSignificantBit 会返回最低有效非零位的索引值。在很多文献内,我们也会称该函数为 lsb 函数或者 ffs 算法(Find first set)。
该函数定义如下:
function leastSignificantBit(uint256 x) internal pure returns (uint8 r) {
require(x > 0);
assembly ("memory-safe") {
// Isolate the least significant bit.
x := and(x, sub(0, x))
// For the upper 3 bits of the result, use a De Bruijn-like lookup.
// Credit to adhusson: https://blog.adhusson.com/cheap-find-first-set-evm/
// forgefmt: disable-next-item
r := shl(5, shr(252, shl(shl(2, shr(250, mul(x,
0xb6db6db6ddddddddd34d34d349249249210842108c6318c639ce739cffffffff))),
0x8040405543005266443200005020610674053026020000107506200176117077)))
// For the lower 5 bits of the result, use a De Bruijn lookup.
// forgefmt: disable-next-item
r := or(r, byte(and(div(0xd76453e0, shr(r, x)), 0x1f),
0x001f0d1e100c1d070f090b19131c1706010e11080a1a141802121b1503160405))
}
}
此处,我们将首先解决 r 的低 5 位的计算。因为低 5 位的计算较为简单。此处我们会使用到一种 de Bruijn Sequences 的东西。我们可以为读者介绍一下这种计算方案。直觉上,计算的复杂度往往高于查表,所以我们会直观想到是否存在一种哈希算法可以提取出每一个二进制数据的哈希值,然后我们根据哈希值直接查表获得计算结果?但是该如何构造一种简单有效的哈希算法?此处,我们会发现存在 de Bruijn Sequences 常数。该常数允许我们仅使用简单的乘法构造出我们预期的哈希算法。此处,我们可以举出一个案例。
在 神奇的德布鲁因序列 中包含对
de Bruijn Sequences的更加详细的介绍,建议读者首先阅读此篇文章
假如我们需要对一个 8 bit 的数字使用 de Bruijn Sequences 进行计算,我们不加解释的直接给出在 8bit 条件下,de Bruijn Sequences 的数值为 0b00011101。所使用的哈希表格如下:
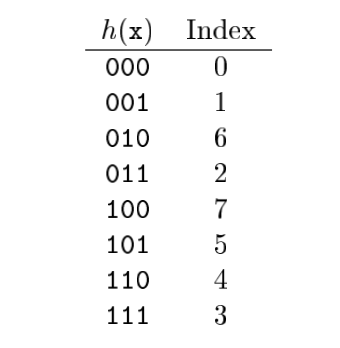
假如我们需要对 0b10010000 计算最低有效位。我们首先需要对输入进行处理,处理方法为 v & (-v) ,处理完成后,0b10010000 会转化为 0b00010000 ,我们可以看到处理最低有效位,其他的位都被清零。我们可以看到上文给出的 leastSignificantBit 就使用了 and(x, sub(0, x)) 的操作来处理输入,但是需要注意上文给出的 leastSignificantBit 存在 require(x > 0); 的限制,所以可以直接使用 and(x, sub(0, x)),而更加通用的没有任何限制的处理方法应该是 x := and(x, add(not(x), 1)),该处理方法无视 x 的正负属性。
我们可以直接计算 0b00010000 * 0b00011101 = 0b11010000,此处的 0b00011101 是 de Bruijn Sequences 常数。此处我们限定计算域为 8 bit。然后,我们此处使用了 3 位的哈希表格,所以我们需要将 0b11010000 右移 5 位,获得的结果为 0b110,查表可以获得最低有效位索引为 4,该数值是正确的。
我们首先考虑在 EVM 内使用上述算法可以搜索的最大位数。显然,我们使用 de Bruijn Sequences 算法所占据最大空间的是哈希表格。考虑搜索 5bit,此时共有 32 种索引([0, 32]),每种索引值需要占据 5 bit,所以理论上 160bit 就可以承载整个表格。而搜索 6bit,则有 64 种索引,索引占据 6bit 空间,所以理论上需要 64 * 6 = 384 bit 空间。
按照需要,我们可以写出以下 z3 求解方法:
from z3 import BitVec
from z3 import solve
l = BitVec('l', 256)
q = BitVec('q', 256)
byte_lookup = lambda i, x: (x >> ((31 - (i & 31)) << 3)) & 0xff
solve(
*[
byte_lookup((0x077CB531 * (1 << i)) >> 27, l) == i
for i in range(32)
], byte_lookup(0, l) == 0,
)
此处,我们直接使用了 bithack 内提供的常数。此外,读者也可以在 De Bruijn Sequence 的 Wiki 页面内找到更多常数,该页面给定了 8bit / 16bit / 32bit /64bit 下的常数。
另外,需要注意的,因为 de Bruijn Sequences 实际上只会对只包含最低有效位的数值操作,所以此处我们的搜索空间并不大,只是包含 31 种存在最低有效位的情况,这些情况下的输入可以直接使用 1 << i 表示。此外还存在一种不包含最低有效位的情况,对于这种情况,我们单独编写了 byte_lookup(0, l) == 0 的约束条件。
可能有读者会感觉此处的 (0x077CB531 * (1 << i)) >> 27 可能可以化简,比如是否可能化简为某种除法,因为左移 32bit 可以转化为整除 2 ^ 32 数值。但是我们似乎很难手动化简,此处我们可以直接尝试使用 z3 求解:
solve(
*[byte_lookup(UDiv(q, 1 << i), l) == i for i in range(32)],
byte_lookup(0, l) == 0
)
此处直接引入了 z3 内的无符号除法 UDiv 函数。此处我求解获得结果为:
[l = 54979636509525628055274853402760638687880834366786308908604839894503986711,
q = 2947691744]
此结果也是与 solady 给出的结果不一致,但是读者可以自行测试 solady 给出的结果也是符合上述约束的。根据上述求解结果,我们就可以获得 solady 内部的以下代码:
r := or(r, byte(and(div(0xd76453e0, shr(r, x)), 0x1f),
0x001f0d1e100c1d070f090b19131c1706010e11080a1a141802121b1503160405))
而 r 的较高的 5bit 的求解,在之前使用了二分的方法,但是 Adrien Husson 在 20% cheaper find-first-set bit using a new de Bruijn-like sequence 给出了一个基于 de Bruijn-like sequence 的更优方案。首先,我们需要理解 de Bruijn Sequences 算法的核心,该算法本质上是因为 de Bruijn Sequences 是一个特殊的结构,可视化来看该结构是一个环:

上述展示了 0000101101001111 的结构,我们可以在上述环结构内任意选择一个位置,并以此位置顺时针连续取出 4 个位元,我们可以发现无论从环的那个位置开始,任意连续的 4 个位元都是不同的。在上文内,我们就使用了此性质。
现在,我们的目标是搜索 r 的最高的 3 位,换句话说,我们希望搜索最低有效位所在的块位置:
bit pos in x 255-224 223-192 ... 63-32 31-0
block num in x 7 6 1 0
由此,我们希望构造一种特殊的 de Bruijn-like sequence ,在该序列内,某一个区间内存在同一个模式。(在 de Bruijn Sequences 是每一个位都存在自己的独立模式)。
我们先给出一个构建好的 de Bruijn-like sequence 序列 m = 0x924924924e739ce736db6db6fffffffff88888842aaaaaaaaebaebaeb060c183 ,该序列可以使用以下更加易读的方法表示:
Block 0 10010010010010010010010010010010 -> 100100 / 001001 / 010010 /
Block 1 01001110011100111001110011100111 -> 010011 / 100111 / 001110 / 011100 / 111001 / 110011 / 100110
Block 2 00110110110110110110110110110110 -> 100110 / 011011 / 110110 / 101101 / 110111 / 101111 / 011111
Block 3 11111111111111111111111111111111 -> 111111
Block 4 11111000100010001000100010000100 -> 111110 / 111100 / 111000 / 110001 / 100010 / 000100 / 001000 / 010001 / 010000 / 100001 / 000010 / 000101
Block 5 00101010101010101010101010101010 -> 001010 / 010101 / 101010
Block 6 10101110101110101110101110101110 -> 101011 / 010111 / 101110 / 011101 / 111010 / 110101 / 010110
Block 7 10110000011000001100000110000011 -> 101100 / 011000 / 110000 / 100000 / 000001 / 000011 / 000110 / 001100
在上述的 -> 后面代表该块所对应 6 位模式。比如我们最后使用 x * m 获得 010011 的结果,那么我们认为 x 位于 Block 1 内部。此处需要注意衔接部分,比如 Block 0 的最低 2 位 10 需要与 Block 1 的最高 4 位 0100 衔接,我们应确保衔接后的结果 100100 被划分到正确的位置。另外,在 Block7 是一个特殊情况,Block 7 内的的最低位需要与 0 衔接,比如 Block 7 的最低 2 位 11,需要衔接 4 位 0 ,结果为 110000。
有读者可能会疑惑,我们上文提到
de Bruijn Sequences是一个环结构,那么为什么Block 7不是和Block 0衔接?这是因为我们使用(x * m) >> 250获得最后的 6 位模式结果。
读者可能疑惑为什么此处使用 6 位模式,而不是 5 位模式,这是因为 5 位模式提供的模式数量为 32 种,32 种模式无法构造出上述结果。我们在上述结果内使用了 48 种不同的模式。当然,可能有读者认为这是事后诸葛亮的说法,但读者可以自行尝试使用 5 位构造出一个符合要求的 m 是不可能的。建议读者直接使用纸和笔进行构造。
当我们确定使用 m = 0x924924924e739ce736db6db6fffffffff88888842aaaaaaaaebaebaeb060c183 后,我们需要构造检索表,即在已知 101011 后,我们需要在表内查询到 010010 对应 Block 1。此处最简单的方案是直接查询,即在 uint256 的 0b010010(对应 18) 索引位置插入 0b000。然后我们会发现 Block 1 对应的 010011,则要求 uint256 的索引为 19(0b010011) 为 0b001。显然,假如采取直接映射的方案 010010 和 010011 存在冲突。
我们使用的解决方案很简单,直接将 6 位模式左移 2 位,将 010010 模式映射到 uint256 的 0b01001000 (对应十进制数值为 72) 位置,而 010011 模式映射到 uint256 的 0b01001100 (对应十进制数值为 76) 位置。此时 76 - 72 = 4,我们有充足的空间进行非冲突写入。
上述描述可以转化为以下 yul 代码:
let m := 0x924924924e739ce736db6db6fffffffff88888842aaaaaaaaebaebaeb060c183
let pattern := shr(250,mul(x,m))
pattern := shl(2,pattern) // left extend pattern
let h := ???
let c := shr(252,shl(pattern,h))
c := shl(5,c)
此处的 h 就是我们所需要的用于索引值查找的 uint256。而此处使用 shl(pattern,h) 通过左移进行查找,最后使用 shr(252,shl(pattern,h)) 清理除了检索出的 3 位外的其他位置。此处我们不知道 h 的数值,我们可以直接使用 z3 进行查找。以下代码来自 Solady 的作者 Vectorized 在 PR 内部的补充:
from z3 import *
import math
def lookup(j, m, h):
j = j & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
t = (m * j) & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
t = (t >> 250)
t = (t << 2)
t = (h << t) & 0xffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
t = (t >> 252)
# t = q >> t
return t
m = BitVec('m', 512)
h = BitVec('h', 512)
solve(
*[
lookup(1 << i, m, h) == ((int(math.log2(1 << i)) >> 5) & 0b111)
for i in range(256)
],
lookup(1 << 256, m, h) == 0b1000,
m >> 256 == 0, h >> 256 == 0
)
上述代码也对 m 进行了检索。上述代码内的 lookup(1 << 256, m, h) == 0b1000 实际上在处理输入为 0 的情况,此时返回值为 0b1000。0b1000 会在后续步骤中被转化为 0b100000000 ,由于返回值为 uint8,所以最高位的 1 会被清除。
该方案背后的数学原理似乎涉及到离散数学领域中的 Universal Cycle Constructions 等内容。如果读者对此内容感兴趣,可以尝试阅读该领域最权威的网站 De Bruijn Sequence and Universal Cycle Constructions 内提供的内容。 $$ x = \mod{x_0} $$
FullMath
FullMath 库内部包含一个有趣的函数 mulDiv(uint256 a, uint256 b, uint256 denominator),这个函数会执行 a * b / denominator 的计算,读者可能感觉实现起来应该非常简单,但实际上该函数实现是非常复杂的,原因在于 a * b 这部分是全精度计算的,即 a * b 的结果实际上是一个 uint512 类型的变量。这种超过 256 位的全精度计算使得代码变得极其复杂。
我们在下文将首先介绍全精度的乘法实现,然后介绍如何使用对全精度乘法的结果进行除法计算。
在介绍全精度乘法之前,我们首先介绍一个基础的定理,即中国剩余定理(Chinese Remainder Theorem)。所谓的中国剩余定理是用来解决同余式问题的。举出一个简单例子,假设存在正整数 $x$,$x$ 的特性是除以 7 的余数为 4,除以 3 的余数为 1,那么 $x$ 的值是多少?我们可以使用模除表示以上例子: $$ \begin{align} x &\equiv 4\mod 7 \newline x &\equiv 1\mod 3 \end{align} $$ 求解上述方程就需要使用中国剩余定理,我们可以使用以上方程的求解展示一下:
第一步,进行如下计算: $$ N = 7 \times 3 = 21 \newline N_1 = 21 / 7 = 3 \newline N_2 = 21 / 3 = 7 $$ 第二步,使用扩展欧几里得算法: $$ \begin{array}{cccc} 1 = & 5 \cdot 3 & + & -2 \cdot 7 \newline 1 = & 1 \cdot 7 & + & -2 \cdot 3 \end{array} $$ 最后,我们可以获得解为 $x = 4 \cdot 5 \cdot 3 + 1 \cdot 1 \cdot 7 = 67$。如果读者不是完全理解扩展欧几里得算法等,请阅读 中国剩余定理 一节。我们可以将上述流程使用数学符号描述。我们希望求解以下方程,注意以下方程内的 $x < m_0 \cdot m_1$ 并且 $m_0$ 和 $m_1$ 互质: $$ \begin{align} x = x_0 \mod m_0 \newline x = x_1 \mod m_1 \end{align} $$ 我们仍是先进行 $N$ 的计算:
$$ \begin{align} N &= m_0 \cdot m_1 \ N_0 &= N / m_0 = m_1 \ N_1 &= N / m_1 = m_0 \end{align} $$
第二步进行扩展欧几里得算法:
$$
\begin{array}{cccc}
1 = & s_0 \cdot m_1 & + & t_0 \cdot m_0 \newline
1 = & s_1 \cdot m_0 & + & t_1 \cdot m_1
\end{array}
$$
此处,我们可以考虑基于上述公式化简 $s_0$ 和 $s_1$。
$$
\begin{align}
1 &= s_0 \cdot m_1 + t \cdot m_0 &\implies \newline
1 \mod m_0 &= s_0 \cdot m_1 \mod m_0 &\implies \newline
s_0 &= m_1^{-1} \mod m_0
\end{align}
$$
同理也可以获得 $s_1 = m_0^{-1} \mod m_1$。最终可以获得:
$$
x = (x_0 \cdot s_0 \cdot m_1 + x_1 \cdot s_1 \cdot m_1) \mod {m_0 \cdot m_1}
$$
在以上公式内进行的最后一部分 $\mod {m_0 \cdot m_1}$ 是为了满足 $x < m_0 \cdot m_1$ 的条件。考虑一种特殊情况,即 $m_1 = m_0 - 1$。此时,存在
$$
\begin{align}
s_0 = m_1^{-1} &\mod m_0 = m_1\newline
s_1 = m_0^{-1} &\mod m_1 = 1
\end{align}
$$
在这种情况下,$x$ 的计算可以简化为:
$$
x = (x_0 \cdot m_1^2 + x_1 \cdot m_0) \mod m_0 \cdot m_1
$$
我们给定此处的 $m_0 = 2^{256}$ ,发现 $x$ 是一个 512 精度的数字,而 $x_0$ 和 $x_1$ 则都是 256 位精度。我们离全精度乘法更近了一步。我们继续化简 $x$ 的表达式。在以上公式内带入 $m_1 = m_0 - 1$ 可得:
$$
x = x_0 + (x_1 - x_0) \cdot m_0 \mod m_0^2 - m_0
$$
mod 计算比较麻烦,此处我们可以化简 $x$ 为:
$$
x = x_0 + (x_1 - x_0) \cdot m_0 + c(m_0^2 - m_0)
$$
因为模除的性质,只有在 $x_1 < x_0$ 时, $x_0 + (x_1 - x_0) \cdot m_0 < 0$。所以此处的 $c$ 在 $x_1 < x_0$ 时,$c = 1$,其他情况下,$c = 0$。
下一步,$x$ 是 512 位精度,我们需要使用 256 位精度表示,所以我们设 $x$ 的低 256 位为 $r_0$ 而高 256 位为 $r_1$。那么 $x = r_0 + 2^{256} \cdot r_1 = r_0 + m_0 r_1$。此处使用了上文给定的 $m_0 = 2^{256}$ 。
那么我们可以得到: $$ r_0 + m_0 r_1 = x_0 + (x_1 - x_0) \cdot m_0 + c(m_0^2 - m_0) $$ 显然,$r_0 = x_0$,那么可以获得 $$ \begin{align} m_0 r_1 &= (x_1 - x_0) \cdot m_0 + c(m_0^2 - m_0)\newline r_1 &= x_1 - x_0 + cm_0 - c\newline r_1 &= x_1 - x_0 - c \end{align} $$ $cm_0$项消失的原因是 $r_1$ 只有 256 位精度,换言之上述计算都存在隐含的 $\mod m_0$ 的计算。如此,我们也获得了 $x$ 的 256 位表达形式。
最后,我们希望知道假如计算 $a \cdot b$ 的结果,我们该如何计算 $x_0$ 和 $x_1$,我们重温一下 $x$ 的早期形式($m_0 = 2^{256},m_1 = 2^{256} - 1$): $$ x = (x_0 \cdot m_1^2 + x_1 \cdot m_0) \mod m_0 \cdot m_1 $$ 显然,假如 $x = a \cdot b$,那么 $x_0 = (a \cdot b) / 2^{256}, x_1 = (a \cdot b) / (2^{256} - 1)$。上述数学推导总结为: $$ \begin{align} x_0 &= (a \cdot b) / 2^{256} \ x_1 &= (a \cdot b) / (2^{256} - 1) \ r_0 &= x_0\newline r_1 &= x_1 - x_0 - c \end{align} $$ 上述 $c$ 只有在 $x_1 < x_0$ 时才会出现,数值为 $1$。以上数学推导可以转化为以下算法:
function mul512(uint256 a, uint256 b) public pure returns(uint256 r0, uint256 r1) {
assembly {
let mm := mulmod(a, b, not(0)) // mm = x1
r0 := mul(a, b) // r0 = x0
r1 := sub(sub(mm, r0), lt(mm, r0))
}
}
此处计算 $x_1 = (a \cdot b) / (2^{256} - 1)$ 使用了 mulmod 操作码来节省 gas。
接下来,我们主要讨论 512bit 除以 256bit 的除法。设使用 $(prod_0, prod_1)$ 构成的 $a \cdot b$ 的 512 位计算结果除以 256 位的 $denominator$,那么结果 $x$ 可以表示为: $$ x = \left\lfloor \frac{prod_1 \cdot 2^{256} + prod_0}{denominator}\right\rfloor $$ 第一步,我们希望希望 $x$ 是 $denominator$ 的整数倍,或者说 $prod_1 \cdot 2^{256} + prod_0$ 与 $denominator$ 的除法结果没有余数。
uint256 remainder;
assembly {
remainder := mulmod(a, b, denominator)
}
// Subtract 256 bit number from 512 bit number
assembly {
prod1 := sub(prod1, gt(remainder, prod0))
prod0 := sub(prod0, remainder)
}
上述代码进行此逻辑,我们使用 EVM 原生操作码 mulmod 计算出 $a \cdot b \mod denominator$ 的结果,该结果是 $prod_1 \cdot 2^{256} + prod_0$ 与 $denominator$ 的除法余数。所以,我们可以使用 $(prod_1, prod_0)$ 减去上述 mulmod 的计算结果 remainder 。上述的 gt(remainder, prod0) 是为了 remainder > prod0 时,实现减法过程中的退位处理,即 $prod_1 - 1$ 且 $prod_0 + 2^{256} - remainder = prod_0 - remainder \mod 2^{256}$。完成以上代码后,我们可以认为:
$$ x = \frac{prod_1 \cdot 2^{256} + prod_0}{denominator} $$
由于余数已经被处理,所以我们不再需要向下取整。获得以上公式后,我们希望进行化简:
$$ \frac{prod_1 \cdot 2^{256} + prod_0}{denominator} = \frac{prod_1 \cdot 2^{256} / c + prod_0 / c}{denominator / c} $$
我们希望对分子和分母同时除以某一个数字 $c$,进行放缩。我们使用的 $c$ 的取值是小于 $denominator$ 的最大的可表示为 2 的幂的因子,我们可以使用以下代码计算:
// Always >= 1.
uint256 twos = (0 - denominator) & denominator;
// Divide denominator by power of two
assembly ("memory-safe") {
denominator := div(denominator, twos)
}
// Divide [prod1 prod0] by the factors of two
assembly ("memory-safe") {
prod0 := div(prod0, twos)
}
twos 就是我们需要的 $c$ 的数值。关于 twos 的计算,我们可以使用以下方法。对于 $denominator$ 可以表示为如下形式:
$$ \text{denominator} = 2^k \times \text{odd} $$
其中,$\text{odd}$ 是一个奇数,我们的 twos 实际上就是上述公式中的 $2^k$。在二进制计算内,乘以 $2^k$ 可以视为将某一个数字左移 $k$ 位,那么我们可以获得如下 denominator 二进制表示:
$$ \text{denominator} = \underbrace{b_n b_{n-1} \cdots b_{k+1}}_{任意位(odd)}\ \underbrace{1}_{第k位}\ \underbrace{0 \cdots 0}_{后k位} $$
而 0 - denominator 实际上等同于 ~denominator + 1 ,此处的 ~ 代表取反操作。执行 0 - denominator 后的结果为:
$$ \underbrace{1 \cdots 1}_{前n-k位} \underbrace{0}_{第k位} \underbrace{1 \cdots 1}_{后k位} + 1 = \underbrace{1 \cdots 1}_{前n-k位} \underbrace{1}_{第k位} \underbrace{0 \cdots 0}_{后k位} $$
最后,我们可以执行 & denominator 操作获得 twos 的数值:
$$ \text{twos} = \underbrace{0 \cdots 0}_{前n-k位} \underbrace{1}_{第k位} \underbrace{0 \cdots 0}_{后k位} $$
由此,我们认为 uint256 twos = (0 - denominator) & denominator;。关于为什么 twos 就是最大的可表示为 2 的幂的因子,读者可以自行使用反证法证明。
获得 twos 的具体数值后,我们计算 $prod_1 \cdot 2^{256} / c$ 和 $prod_0 / c$ 的数值:
// Divide [prod1 prod0] by the factors of two
assembly ("memory-safe") {
prod0 := div(prod0, twos)
}
// Shift in bits from prod1 into prod0. For this we need
// to flip `twos` such that it is 2**256 / twos.
// If twos is zero, then it becomes one
assembly ("memory-safe") {
twos := add(div(sub(0, twos), twos), 1)
}
prod0 |= prod1 * twos;
对于 $prod_0 / c$ 的计算直接使用 div(prod0, twos) 即可,而 prod1 则需要首先计算 2**256 / twos 的数值。此处我们使用 sub(0, twos) 获得 2 ** 256 - twos 的数值,然后使用 div(sub(0, twos), twos) 计算 2 ** 256 / twos - 1,最后使用 add(div(sub(0, twos), twos), 1) 计算获得 2**256 / twos 的数值。
最后,我们将 prod1 和 prod0 的数值放到一起 prod0 |= prod1 * twos;。该计算实际上等同于 prod1 * twos + prod0。这是因为 $twos = 2^k$。那么:
$$
prod1 \cdot \frac{2^{256}}{twos} + \frac{prod0}{twos} = prod1 \cdot 2^{256 - k} + \frac{prod0}{2^k}
$$
我们可以看到在二进制计算内,对于 $2^m$ 类型的数字的乘除都可以视为位移。 prod1 位于高位,而 prod0 位于低位,两者并没有交叉,所以我们可以直接使用 | 计算合并。
那么我们最后只需要计算 prod0 / denominator。此处我们首先需要计算 1 / denominator 的数值,该数值实际上可以视为在 $2^{256}$ 有限域内求逆元的过程。求解逆元就是计算 1 / a 的数值。假如我们在自然数范围内求解 1 / a 的数值,我们可以使用 Newton–Raphson division 方法,该方法使用:
$$
r_{i + 1} = r_i(2 - a \cdot r_i)
$$
上述公式每次迭代都可以增加一倍精度,所以计算到 $r_8$ 就可以将精度增加到 $2^{256}$ 的范围。但是我们此处需要在有限域内进行计算,根据 Hensel’s lemma 定理,上述方法在有限域内也是有效的,可以使用以下公式:
$$
r_0 = 1 \newline
r_{i+1} = r_i \cdot (2 - a \cdot r_i) \mod 2^{2^i}
$$
根据 Efficient long division via Montgomery multiply 论文,我们可以直接使用 $r_2 = 3 * a ^ 2$ 进行快速计算。
uint256 inv = (3 * denominator) ^ 2;
// Now use Newton-Raphson iteration to improve the precision.
// Thanks to Hensel's lifting lemma, this also works in modular
// arithmetic, doubling the correct bits in each step.
inv *= 2 - denominator * inv; // inverse mod 2**8
inv *= 2 - denominator * inv; // inverse mod 2**16
inv *= 2 - denominator * inv; // inverse mod 2**32
inv *= 2 - denominator * inv; // inverse mod 2**64
inv *= 2 - denominator * inv; // inverse mod 2**128
inv *= 2 - denominator * inv; // inverse mod 2**256
// Because the division is now exact we can divide by multiplying
// with the modular inverse of denominator. This will give us the
// correct result modulo 2**256. Since the preconditions guarantee
// that the outcome is less than 2**256, this is the final result.
// We don't need to compute the high bits of the result and prod1
// is no longer required.
result = prod0 * inv;
return result;
最后使用 result = prod0 * inv; 计算结果即可。
TickMath
TickMath 数学库中主要包含对数计算和指数计算。
对数计算
在对数计算中,我们一般使用换底公式将任意的对数计算转化为 $\log_2x$ 的计算:
$$
\log_bx=\frac{\log_2x}{\log_2b}
$$
那么我们面前最核心的问题是如何计算任意数值的 $log_2 x$ 的结果。考虑 $x$ 是一个二进制表示的整数,且我们希望 $\log_2 x$ 的结果也是一个整数,那么最简单的方案就是使用上文介绍的 mostSignificantBit 算法。具体的数学推导如下:
$$
2^n \le x < 2^{n + 1}\implies n \le \log_2x < n + 1
$$
我们可以直接使用 msb(x) 计算获得 $n$ 的数值。但在实际过程中,我们一般在 solidity 中使用定点小数进行小数的表示,比如我们希望表示一个小数 $x$。以 Uniswap V4 中使用 128bit 定点小数为例,对于一个小数 $x$,我们会使用以下方法表示:
$$
x = m \times 2^{-128}
$$
其中 $m$ 就是我们在 solidity 中存储和使用的整数。比如我们希望在 solidity 中表示 1.21,该小数在 solidity 中实际被存储为 $m = 1.21 \times 2^{128} = 411741663974335528701425078846147788800$。
对于任意的 128 bit 定点小数 $x$,我们也可以将 $x$ 使用以下方法表示: $$ x = n_0 \times 1 + n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} + \dots + n_{128}\times \frac{1}{2^{128}} $$ 上述定义中除了 $n_0$ 外的 $n_i \in {0, 1}(i \ne 0)$。这其实是在二进制系统内部生效的,如下:
$$ x = \overbrace{\underbrace{1 \cdots 1}_{1}}^{\text{第 255 - 128 位}}\ \overbrace{\underbrace{1}_{\frac{1}{2}}}^{第127位}\ \overbrace{\underbrace{0}_{\frac{1}{4}}}^{第126位}\ \cdots \overbrace{\underbrace{0}_{\frac{1}{2^{128}}}}^{第0位} $$
我们认为第 255 - 128 位表示的数字为 $n_0$,而第 95 位上的数字为 $n_1$,所以上文定义中除了 $n_0$ 外,其他的 $n_i$ 的数值只可能为 0 或 1。
在介绍完定点小数的性质后,我们需要尝试对定点小数进行 log2 数学计算。第一步,我们可以先计算 $n_0$ 的数值,该数值的计算依赖以下公式:
$$
\log_2x=\log_2 (m \times 2^{-128})=\log_2m - 128
$$
此处 $\log_2 m$ 可以直接使用 mostSignificantBit 算法计算,即 $n_0 = \text{msb}(m) - 128$上述计算在 Uniswap V4 内使用了如下代码:
int256 log_2 = (int256(msb) - 128) << 64;
上述的位移操作是为了 log_2 的定点小数二进制表示,Uniswap V4 输出的 log_2 数值为 64bit 定点小数,所以此处需要将计算获得的 $n_0$ 向左移动 64 位。
接下来,我们需要对 log_2 的小数部分进行计算,上文中提及 log_2 是 64bit 定点小数,根据上文中的二进制表示方法,log_2 可以被表示为:
$$
\log_2x = n_0 + n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} + \dots + n_{64}\times \frac{1}{2^{64}}
$$
目前在已知 $n_0$ 的情况下,我们需要计算 $n_1$ 等数值。此处我们先忽略 $n_3$ 及以后的数值,可以获得以下数学等式:
$$
\begin{align}
\log_2 x &= n_0 + n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} \newline
\log_2 x - n_0 &= n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} \newline
\log_2 \frac{x}{2^{n_0}} &= n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4} \newline
\log_2 r &= n_1 \times \frac{1}{2} + n_2 \times \frac{1}{4}\newline
\end{align}
$$
在上述公式内,我们记 $r = \frac{x}{2^{n_0}}$。因为 $x$ 和 $n_0$ 的数值已知,所以 $r$ 是可以计算的。此处在右侧存在 $n_1 \times \frac{1}{2}$ 因子,这个 $\frac{1}{2}$ 并不友好,我们进行以下数学转化:
$$
\begin{align}
\log_2 r^2 = 2 \log_2 r = n_1 + n_2 \times \frac{1}{2}
\end{align}
$$
接下来,只要 $\log_2 r^2 \geq 1$,我们就可以认为 $n_1 = 1$。显然,当 $r^2 > 2$,$\log_2 r^2 \geq 1$ 成立,此时 $n_1 = 1$,否则 $n_1 = 0$。
因为 $n_2 \times \frac{1}{2}$ 因子的存在,所以有可能导致 $\log_2 r^2 \geq 1$。
另外上述的“显然”可以使用以下方法推导: $$ \log_2 x > 1 \implies 1 + \log_2\frac{x}{2} > 1 \implies \log_2\frac{x}{2} > 0\implies x > 2 $$
当我们完成 $n_1$ 的计算后,我们发现: $$ \log_2 r^2 = n_1 + n_2 \times \frac{1}{2} $$ 上述计算结果中的 $n_1$ 已知,需要计算 $n_2$,这与最初的 $\log_2 x = n_0 + n_1 \times \frac{1}{2}$ 实质上是一致的,所以此处我们可以将上述流程直接递推。或者更加简单来说,上述流程构成了一个循环,我们可以直接在 solidity 中通过循环完成 $n_1$ 至 $n_{128}$ 的计算。
至此我们就完成了 $\log_2$ 函数的计算基础原理的数学推导。我们可以汇总为以下步骤:
- 使用
msb算法获得结果的整数部分,并定义 $r = x$,此处的 $x$ 代表函数的输入值 - 循环计算 $r = \frac{r}{2^{n_{i-1}}}$ ,并根据 $r^2$ 与 2 的关系判断 $n_i$ 的数值,获得 $n_i$ 数值后重新计算 $r$
接下来,我们可以看看 Uniswap V4 的实现方法。第一步就是使用 msb 算法进行 $n_0$ 的计算,方法如下:
uint256 price = uint256(sqrtPriceX96) << 32;
uint256 r = price;
uint256 msb = BitMath.mostSignificantBit(r);
int256 log_2 = (int256(msb) - 128) << 64;
此处比较有趣的是为了进一步保障计算的精度,我们将 sqrtPriceX96 的小数部分扩展为 128bit。然后直接使用 BitMath 库中的 mostSignificantBit 函数计算 msb 的结果。最后使用 $\log_2x=\log_2 (m \times 2^{-128})=\log_2m - 128$ 计算出 log_2 的数值。此处的 log_2 是一个 64 位定点小数,所以此处将计算出的 $n_0$ 左移了 64 位。
随后,我们需要计算 $r = \frac{x}{2^{n_0}}$。计算过程如下: $$ r = \frac{x}{2^{n_0}} = \frac{x}{2^{msb - 128}} = \begin{cases} \frac{x}{2^{msb - 128}} &msb \ge 128 \ x \times 2 ^{128 - msb} &msb < 128 \end{cases} $$ 可以注意到因为 $x$ 是一个 128 bit 定点小数,所以 $r$ 本身也是一个 128bit 定点小数。但我们希望将 $r$ 重整为一个 127bit 定点小数。关于为什么需要重整,我们会在下文介绍。重整是非常简单的,只需要 $r_{127bit} = r_{128 bit} \times 2$ 即可。根据上述计算,可以获得如下代码:
if (msb >= 128) r = price >> (msb - 127);
else r = price << (127 - msb);
在已知 $n_0$ 和 $r$ 的情况下,我们可以通过以下迭代算法获得 $n_1$ 的数值:
assembly ("memory-safe") {
r := shr(127, mul(r, r))
let f := shr(128, r)
log_2 := or(log_2, shl(63, f))
r := shr(f, r)
}
我们首先需要计算 $r^2$ 的数值,上述代码内使用了 mul(r, r) 进行计算,计算出的 $r^2$ 是一个 254bit 的定点小数。显然,作为一个 254bit 的定点小数,$r^2$ 的整数部分只有可能是 00 / 01 / 10 / 11。此处只有整数部分是 10 和 11 的情况才是 $r^2 > 1$ 的情况。简单来说,我们只需要获得 mul(r, r) 的第 256 位的数值就可以知道 $n_1$ 的数值。在具体操作时,我们只需要 $r^2$ 左移 255 bit 就可以获得 $n_1$ 的数值。上述代码通过两行代码实现这个过程:
r := shr(127, mul(r, r))
let f := shr(128, r)
为了方便下次计算,所以此处使用 r := shr(127, mul(r, r)) 将 $r^2$ 恢复为 127bit 定点小数并进行了重赋值处理。接下来,shr(128, r) 对重赋值后的 r 左移 128bit 获得了 $n_1$ 的数值,此处使用 f 表示。最后,我们使用 log_2 := or(log_2, shl(63, f)) 将 f 的数值写入 $n_0$ 本身所在的位置。
在最后,我们需要计算 $r$ 的新数值 $r = \frac{r}{n_1}$。此处使用的方法是 r := shr(f, r)。因为 f 只能是 1 或 0 ,所以此处也不需要对计算出的 r 进行精度重整计算。在 Uniswap V4 中,我们将上述过程进行多次计算,每一次计算都可以为 log_2 增加精度。Uniswap V4 总计进行了 14 次精度提升计算。我们会在本节的最后推导为什么需要进行 14 次精度计算。
根据 $\log_bx=\frac{\log_2x}{\log_2b}$ 的计算公式,此处我们需要计算 $1 \div \log_2 \sqrt{1.0001} = \log_{\sqrt{1.0001}} 2$ 的数值,此处我们使用 Python 进行计算。在常规 Python 计算工具无法保证高精度计算下的误差,我们一般使用 mpmath 这种超高精度 Python 库进行相关计算。由于 log_2 就是一个 64bit 定点小数,所以我们最终想要的常数为 $2^{64}log_{\sqrt{1.0001}} 2$,计算过程如下:
>>> from mpmath import mp
>>> mp.dps = 50
>>> mp.log(2, mp.sqrt(1.0001)) * mp.power(2, 64)
mpf('255738958999631990525211.87962332383604348269335754749')
此处计算的结果与 Uniswap V4 在代码中给出的 int256 log_sqrt10001 = log_2 * 255738958999603826347141; 稍有不同,可能是因为 Uniswap 开发团队在计算过程中使用了其他高精度计算工具。值得注意的是,当我们完成 int256 log_sqrt10001 = log_2 * 255738958999603826347141; 计算后,log_sqrt10001 会变成了 128bit 定点小数。在一般的对数计算过程中,计算出 log_sqrt10001 就已经结束了。
但在 Uniswap V4 中,我们只需要将 log_sqrt10001 转化为 tick 。此处就会涉及到上述介绍的对数计算方法的误差问题。在 Uniswap V4 中,tick 是一个整数,所以 log_sqrt10001 转化后 tick 应该考虑 log_sqrt10001 的误差。误差问题也决定了为什么我们会在 Uniswap V4 进行了 14 次精度计算。
令人开心的是,Uniswap 数学库的开发者 ABDK 在 Logarithm Approximation Precision 内详细介绍了具体的误差计算数学原理,但是不幸的是,这篇文章内的所有 latex 公式都没有被正常渲染。后文本质上可以认为是对 ABDK 文章内错误 latex 公式的正确渲染。
我们使用的算法可以使用以下数学公式表达: $$ l_0 (x) = \left\lfloor \log_2 x \right\rfloor $$ 这是我们第一次计算 $\log_2 x$ 整数部分时的数学表达,那么此时我们与 $\log_2 x$ 的误差为: $$ \varepsilon_0(x) = l_0 (x) - \log_2 x \in (-1;+0] $$ 后续每一次对小数部分的计算可以使用以下数学公式表达: $$ l_{i+1}(x) = \left\lfloor \log_2 x \right\rfloor + \frac{1}{2} l_i \left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) $$ 以上公式内的 $\left\lfloor a \right\rfloor_b$ 代表 $a$ 的向下取整为最接近 $b$ 的因子。另外,上述公式内的 $i$ 代表第 i 次计算。此时我们的误差为:
$$ \begin{equation} \begin{split} \varepsilon_{i+1}(x) &= l_{i+1}(x) - \log_2 x \\ &= \left\lfloor \log_2 x \right\rfloor + \frac{1}{2} l_i \left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) - \log_2 \left(2^{\left\lfloor \log_2 x \right\rfloor}\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right) \\ &=\left\lfloor \log_2 x \right\rfloor + \frac{1}{2} l_i \left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) - \left\lfloor \log_2 x \right\rfloor - \log_2 \frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}} \\ &=\frac{1}{2} l_i \left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) - \log_2 \frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}} \\ &=\frac{1}{2} l_i \left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) - \frac{1}{2}\log_2\left(\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right)^2 \\ &=\frac{1}{2} \left(l_i \left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) - \log_2\left(\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right)^2\right) \end{split} \end{equation} $$
在以上计算的基础上,我们发现 $\left\lfloor a \right\rfloor_b$ 并不好处理,所以我们引入 $\alpha$ 和 $\beta$ 用于简化上述计算结果。其中 $\alpha$ 的选择如下:
$$ \left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}} = \frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}} \cdot (1 - \alpha) $$
可以计算出如下结果:
$$ \alpha = \frac{\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}} - \left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}}{\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}} \in \left[0; 2^{-127}\right) $$
同时选择 $\beta$ ,如下:
$$ \left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}} = \left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2 \cdot (1 - \beta) $$
可以计算出如下结果:
$$ \beta = \frac{\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2 - \left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}}{\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2} \in \left[0; 2^{-127}\right) $$
因此,我们可以将 $\varepsilon_{i+1}(x)$ 进一步化简为:
$$ \begin{equation} \begin{split} \varepsilon_{i+1}(x)& = \dots \\ &=\frac{1}{2} \left(l_i \left(\left(\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\cdot (1 - \alpha)\right)^2 \cdot (1 - \beta)\right) - \log_2\left(\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right)^2\right) \\ &=\frac{1}{2} \left(l_i \left(\left(\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right)^2 \cdot (1 - \alpha)^2 \cdot (1 - \beta)\right) \ - \log_2\left(\left(\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right)^2 \cdot (1 - \alpha)^2 \cdot (1 - \beta)\right) +\log_2 \left((1 - \alpha)^2 \cdot (1 - \beta)\right)\right)\\ &=\frac{1}{2}\left(\varepsilon_i\left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) + \log_2 \left((1 - \alpha)^2 \cdot (1 - \beta)\right)\right) \\ &=\frac{1}{2}\left(\varepsilon_i\left(\left\lfloor\left(\left\lfloor\frac{x}{2^{\left\lfloor \log_2 x \right\rfloor}}\right\rfloor_{2^{-127}}\right)^2\right\rfloor_{2^{-127}}\right) + 2 \log_2 \left(1 - \alpha\right) + \log_2 \left(1 - \beta\right)\right) \end{split} \end{equation} $$
基于上述化简结果与 $\alpha$ 和 $\beta$ 的数值,我们可以获得如下范围:
$$ \varepsilon_{i+1}(x) \in\left(\frac{1}{2} \min \varepsilon_i + \frac{3}{2} \log_2\left(1 - 2^{-127}\right);+0\right] =\left(-,2^{-(i + 1)} + 3\left(1-2^{-(i + 1)}\right)\log_2\left(1 - 2^{-127}\right);0\right] $$
这里的 $\min \varepsilon_i$ 取值为 $-2^{-i}$ 。可以想像 $\varepsilon_i$ 最小,代表误差最大(因为 $\varepsilon_i$ 为负数,误差是与绝对值有关的,绝对值越小,误差越小)。当 $\varepsilon_i = -2^{-i}$ 时,我们可以获得上述范围中的 $-2^{-(i + 1)}$ 的因子。而对于 $\frac{3}{2} \log_2\left(1 - 2^{-127}\right)$ 如何变化为 $3\left(1-2^{-(i + 1)}\right)\log_2\left(1 - 2^{-127}\right)$ ,笔者尚不清楚,猜测与 $\alpha$ 和 $\beta$ 的性质有关。
当我们有了 $\log_2 x$ 使用上述算法计算的误差后,我们就可以继续推导在 Uniswap 中通过 sqrtPrice 计算 tick 所需要的算法的误差问题。首先,我们需要确定 $\log$ 函数的误差应该小于多少?这实际上与 tick 直接相关,tick 属于 $[−887272,887272]$ 范围。我们只需要 20bit 和一个符号位就可以涵盖 tick 的表示,所以 tick 本质上是一个 int20 的数据(但是由于 solidity 不支持此类型,所以 tick 在 Uniswap 代码内使用了 int24 类型),其最低精度为 $2^{-20} = 0.000000953$,所以我们在 getTickAtSqrtPrice 内的实现应该保持 $0.0000005$ 即可。由此可得:
$$ \mathtt{getSqrtPriceAtTick} (x) = \gamma(x) \cdot \sqrt{1.0001}^x $$
此处存在 $\gamma(x) \in \left[0.9999995; 1.0000005\right]$。那么 getTickAtSqrtPrice 的情况如下:
$$ \mathtt{getSqrtPriceAtTick}^{-1} (x) = \log_{\sqrt{1.0001}} \frac{x}{\gamma(y)} = \log_{\sqrt{1.0001}} x - \log_{\sqrt{1.0001}} \gamma(y) $$
上述计算中的 $\mathtt{getSqrtPriceAtTick}^{-1} (x)$ 实际上就是 getTickAtSqrtPrice。我们需要计算上述 $\mathtt{getSqrtPriceAtTick}^{-1} (x)$ 的误差:
$$ \log_{\sqrt{1.0001}} x - \log_{\sqrt{1.0001}} \gamma(y) \approx \psi \cdot l_i (x) $$
我们在这里引入了 $\psi$ 作为误差项,代表由于计算方法导致的误差。$\psi$ 的数值就是我们使用 solidity 计算出的 $l_i(x)$ 与实际上对数计算结果的偏差。那么最终的误差应该为:
$$ \begin{equation} \begin{split} \psi &\cdot l_i (x) - \log_{\sqrt{1.0001}} x + \log_{\sqrt{1.0001}} \gamma(y) \\ &= \psi \cdot \left(\log_2 x + \varepsilon_i (x)\right) - \frac{\log_2 x}{\log_2 \sqrt{1.0001}} + \log_{\sqrt{1.0001}} \gamma(y) \\ &= \log_2 x\left(\psi - \frac{1}{\log_2 \sqrt{1.0001}}\right) + \log_{\sqrt{1.0001}} \gamma(y) + \psi \cdot \varepsilon_i (x) \end{split} \end{equation} $$
在 Uniswap V4 内部,$x \in \left[2^{-64}; 2^{64}\right)$。故而以上误差可以简化为
$$ \left(-64\left(\psi - \frac{1}{\log_2 \sqrt{1.0001}}\right) + \psi \cdot \left(-2^{-i} + 3\left(1-2^{-i}\right)\log_2\left(1 - 2^{-127}\right)\right) + \log_{\sqrt{1.0001}} 0.9999995;\ 64\left(\psi - \frac{1}{\log_2 \sqrt{1.0001}}\right) + \log_{\sqrt{1.0001}} 1.0000005\right) $$
观察以上误差构成,$\psi$ 取决于算法迭代的次数,当迭代次数越多,那么误差越小,而 $\log_{\sqrt{1.0001}} 0.9999995$ 和 $\log_{\sqrt{1.0001}} 1.0000005$ 则对误差始终存在贡献,所以我们需要直接在原计算数值的基础上减去:
int24 tickLow = int24((log_sqrt10001 - 3402992956809132418596140100660247210) >> 128);
int24 tickHi = int24((log_sqrt10001 + 291339464771989622907027621153398088495) >> 128);
对于如何确定迭代次数,我们只需要计算上述误差范围,确保最小误差和最大误差在 -1 和 1 内部,读者理论上可以自己编写 Python 代码进行相关计算。ABDK 也提供了最终的 计算结果。我们可以看到迭代 14 次后,就有大概率计算出误差合适的结果。
指数计算
此部分内容大量参考了 深入理解 Uniswap v3 智能合约 (一) 中的相关内容。
在将 tick 转化为 sqrtPrice 过程中,我们需要进行指数计算。在 Uniswap V4 中,我们会计算如下内容:
$$ \sqrt{p} = \sqrt{1.0001}^i = 1.0001 ^{\frac{i}{2}} $$
其中 $i$ 代表 tick 的具体数值。在进行任何数值计算前,我们都需要首先确定取值范围。在 Uniswap V4 中,sqrtPriceX96 由 96 位定点小数表示,且类型为 uint160。理论上,sqrtPriceX96 的取值区间为 $[2^{-96}, 2^{64}]$。事实上,我们只需要求解以下不等式即可:
$$ 2^{-96} < 1.0001 ^{\frac{i}{2}} < 2^{64} $$
利用基础的对数计算,我们可以求解获得:
$$ 2\log_{1.0001} 2^{-96} = -1330909.12 < i < 2\log_{1.0001} 2^{64} = 887272.75 $$
理论上,$i \in [-1330909, 887272]$,但是这是一个不对称区间,同时一旦 sqrtPriceX96 下降到 $2^{-96}$ 附近,那么 sqrtPriceX96 会丧失大量精度。为了保持 sqrtPriceX96 的精度,在实际中,Uniswap V4 使用了 $i \in [-887272, 887272]$ 区间。最终,在 Uniswap V4 中,我们使用了 int24 表示 tick,但需要注意的,实际的 tick 只有 20bit 长度。
对于任何使用二进制表示的 tick 变量,我们可以使用 $\sum_{n=0}^{19}{(x_n \cdot 2^n)}$ (此处的 $x_n$ 代表 tick 第 n 位的位元,其数值只能为 0 或 1)表示 tick 的具体数值。
我们首先考虑 $i < 0$ 的情况,此时:
$$ \begin{equation} \begin{split} \sqrt{p} &= 1.0001^{-\frac{|i|}{2}} = \frac{1}{1.0001^{\frac{|i|}{2}}} = \frac{1}{1.0001^{\frac{1}{2}(\sum_{n=0}^{19}{(x_n \cdot 2^n)})}} \\ &= \frac{1}{1.0001^{\frac{1}{2} \cdot x_0}} \cdot \frac{1}{1.0001^{\frac{2}{2} \cdot x_1}} \cdot \frac{1}{1.0001^{\frac{4}{2} \cdot x_2}} \cdot … \cdot \frac{1}{1.0001^{\frac{524288}{2} \cdot x_{19}}} \end{split} \end{equation} $$
如上文所述,$x_n$ 的数值为 0 或 1,所以我们可以预先计算出 $\frac{1}{1.0001^{\frac{1}{2}}}$ 等数值,通过 $x_n$ 的情况判断是否需要将该数值累乘到最后的结果中。在具体代码实现中,我们会使用 128 bit 定点小数表示中间计算结果以降低误差。在使用 128bit 定点小数的前提下,我们需要预先计算的数值是 $\frac{2^{128}}{1.0001^{\frac{1}{2}}}$ 等。
在计算好预先数值后,我们可以使用如下代码形式进行 $x_n$ 的判断并根据判断结果进行累乘。
if (absTick & 0x2 != 0) price = (price * 0xfff97272373d413259a46990580e213a) >> 128;
当然,我们可以直接编写 Python 代码生成上述形式的代码,使用的 Python 代码如下:
from mpmath import mp
mp.dps = 50
def hexify(x):
return hex(int(x))
d = mp.mpf(1.0001)
c0 = hexify(mp.power(2, 128) / mp.sqrt(d))
print(c0)
for i in range(1, 20):
fixed_number = 2 ** i
print(
"if (absTick & 0x{:X} != 0) ratio = (ratio * {}) >> 128;".format(
fixed_number,
hexify(mp.power(2, 128) / mp.power(d, fixed_number / 2))
)
)
由于 tick 只有 20bit 精度,所以 for i in range(1, 20),我们可以发现上述代码额外打印了 c0 数值,c0 本质上就是 $\frac{2^{128}}{1.0001^{\frac{1}{2}}}$ 的数值,单独计算的原因是因为 $c_0$ 会被用于初始化,并不会和其他 if 语句一致。上述 Python 代码输出为:
0xfffcb933bd6fad9d3af5f0b9f25db4d6
if (absTick & 0x2 != 0) price = (price * 0xfff97272373d41fd789c8cb37ffcaa1c) >> 128;
if (absTick & 0x4 != 0) price = (price * 0xfff2e50f5f656ac9229c67059486f389) >> 128;
if (absTick & 0x8 != 0) price = (price * 0xffe5caca7e10e81259b3cddc7a064941) >> 128;
if (absTick & 0x10 != 0) price = (price * 0xffcb9843d60f67b19e8887e0bd251eb7) >> 128;
if (absTick & 0x20 != 0) price = (price * 0xff973b41fa98cd2e57b660be99eb2c4a) >> 128;
if (absTick & 0x40 != 0) price = (price * 0xff2ea16466c9838804e327cb417cafcb) >> 128;
if (absTick & 0x80 != 0) price = (price * 0xfe5dee046a99d51e2cc356c2f617dbe0) >> 128;
if (absTick & 0x100 != 0) price = (price * 0xfcbe86c7900aecf64236ab31f1f9dcb5) >> 128;
if (absTick & 0x200 != 0) price = (price * 0xf987a7253ac4d9194200696907cf2e37) >> 128;
if (absTick & 0x400 != 0) price = (price * 0xf3392b0822b88206f8abe8a3b44dd9be) >> 128;
if (absTick & 0x800 != 0) price = (price * 0xe7159475a2c578ef4f1d17b2b235d480) >> 128;
if (absTick & 0x1000 != 0) price = (price * 0xd097f3bdfd254ee83bdd3f248e7e785e) >> 128;
if (absTick & 0x2000 != 0) price = (price * 0xa9f746462d8f7dd10e744d913d033333) >> 128;
if (absTick & 0x4000 != 0) price = (price * 0x70d869a156ddd32a39e257bc3f50aa9b) >> 128;
if (absTick & 0x8000 != 0) price = (price * 0x31be135f97da6e09a19dc367e3b6da40) >> 128;
if (absTick & 0x10000 != 0) price = (price * 0x9aa508b5b7e5a9780b0cc4e25d61a56) >> 128;
if (absTick & 0x20000 != 0) price = (price * 0x5d6af8dedbcb3a6ccb7ce618d14225) >> 128;
if (absTick & 0x40000 != 0) price = (price * 0x2216e584f630389b2052b8db590e) >> 128;
if (absTick & 0x80000 != 0) price = (price * 0x48a1703920644d4030024fe) >> 128;
我们可以直接复制黏贴所有的 if 语句进入 solidity 代码。如果读者仔细观察会发现上述常数与 Uniswap V4 代码内的并不一致,这还是因为我们使用的高精度计算库与 Uniswap 开发团队使用的高精度数学计算库不一致导致的,简单计算就会发现,我们获得的常数与 Uniswap V4 的常数误差不高于 1e-18。
对于 price 的初始化,假如 absTick 的第 0 位为 1,那么 price 应该被初始化为 c0,否则初始化为 1。一般来说,我们可以使用 solidity 的三目表达式语法编写初始化代码。但为了节约 gas,Uniswap V4 团队使用了一种无分支的三目表达式写法。如下:
assembly ("memory-safe") {
price := xor(shl(128, 1), mul(xor(shl(128, 1), 0xfffcb933bd6fad37aa2d162d1a594001), and(absTick, 0x1)))
}
上述代码可以被认为是以下函数的特殊版本:
function ternary(bool condition, uint256 x, uint256 y) internal pure returns (uint256 z) {
/// @solidity memory-safe-assembly
assembly {
z := xor(x, mul(xor(x, y), iszero(condition)))
}
}
当 condition = true 时,iszero(condition) = 0,那么 z = xor(x, mul(xor(x, y), 0)) = xor(x, 0) = x;当 condition = false 时,z = xor(x, mul(xor(x, y), 1)) = xor(x, xor(x, y)),因为异或操作满足结合律,所以 x ^ (x ^ y) = x ^ x ^ y = 1 ^ y = y。而 Uniswap V4 的代码原理类似。
最后,我们只需要处理一个问题,在上文中,我们介绍的都是 tick < 0 的情况,假如 tick > 0,我们该如何处理。对于 tick > 0 的情况,我们首先将其视为 tick < 0 的情况处理,然后将结果修正为 tick > 0。对于任何指数计算,都存在:
$$ a^{-b} = \frac{1}{a^b} $$
所以当 tick > 0 时,我们只需要计算 $\frac{2^{256}}{\sqrt{p}}$ 即可。推导如下:
$$ \begin{split} \sqrt{p_{Q128.128}(i)} = 2^{128} \cdot \sqrt{p(i)} = 2^{128} \cdot 1.0001^{\frac{i}{2}} \\ = \frac{2^{128}}{1.0001^{-\frac{i}{2}}} = \frac{2^{256}}{2^{128} \cdot \sqrt{p(-i)}} = \frac{2^{256}}{\sqrt{p_{Q128.128}(-i)}} \end{split} $$
在 Uniswap V4 中,我们使用了如下代码:
if sgt(tick, 0) { price := div(not(0), price) }
sgt 是带符号大小比较,而 sgt(tick, 0) 意味着 tick > 0。最后,我们需要进行类型转化,上文计算出的 $\sqrt{p}$ 是一个 128bit 定点小数,我们要将其转化为 96bit 定点小数。本质上,我们需要进行以下操作:
$$ \mathtt{sqrtP}_{Q64.96}(i) = 2^{96}\mathtt{sqrtP} = \frac{2^{128}\mathtt{sqrtP}}{2^{32}} = \frac{\mathtt{sqrtP}_{Q128.128}(i)}{2^{32}} $$
但是,我们可以看到另一个问题 $\mathtt{sqrtP}_{Q64.96}(i)$ 与 $\mathtt{sqrtP}_{Q128.128}(i)$ 类型不一致,前者为 uint160,而后者为 uint256,但是因为 tick 范围确定,此处并不会出现任何问题。另一个问题是在进行精度转化时的取整策略。此处 Uniswap V4 选择了向上取整。
sqrtPriceX96 := shr(32, add(price, sub(shl(32, 1), 1)))
向上取整的方法就是在 price 基础上增加 sub(shl(32, 1), 1)。
最后,我们讨论一个简单的问题,即如何计算 absTick。比较正常的方法是使用 if 分支语句判断,但是 Uniswap 使用了一种无分支方法,如下:
assembly ("memory-safe") {
tick := signextend(2, tick)
// mask = 0 if tick >= 0 else -1 (all 1s)
let mask := sar(255, tick)
// if tick >= 0, |tick| = tick = 0 ^ tick
// if tick < 0, |tick| = ~~|tick| = ~(-|tick| - 1) = ~(tick - 1) = (-1) ^ (tick - 1)
// either way, |tick| = mask ^ (tick + mask)
absTick := xor(mask, add(mask, tick))
}
第一行中的 tick := signextend(2, tick) 的目的是为了清理高位垃圾数值,同时将 int24 类型的 tick 转化为 int256 类型。然后使用 let mask := sar(255, tick) 观察当前 tick 的正负情况,原理就是在 EVM 内部使用反码表示负数,当最高位为 1 时则代表负数。最后使用异或计算绝对值,具体原理实际上与上文介绍的 ternary 算法一致。